개요
다음은 2011년 5급 국가공무원 민간경력자 일괄채용 제1차 시험 자료해석영역 력책형 18번 문제다.
문제
문 18. 다음 <표>와 <그림>은 어느 지역의 교통사고 발생건수에 대한 자료이다. 이에 대한 <보기>의 설명 중 옳은 것을 모두 고르면?
<표> 연도별 교통사고 발생건수 현황
(단위: 천건)
|
연 도 구 분 |
2006 | 2007 | 2008 | 2009 | 2010 |
| 전체교통사고 | 231 | 240 | 220 | 214 | 213 |
| 음주교통사고 | 25 | 31 | 25 | 26 | 30 |
<그림> 2010년 교통사고 발생건수의 월별 구성비
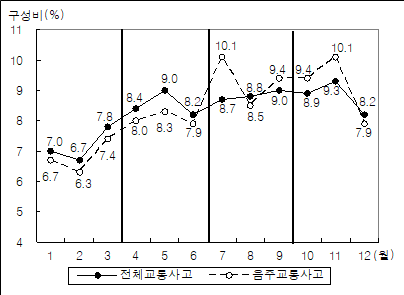
※ 전체(음주)교통사고 발생건수의 월별 구성비(%)
\(=\frac{\text{해당월전체(음주)교통사고발생건수}}{\text{해당연도 전체(음주)교통사고발생건수}}×100\)
| 보기 |
| ㄱ. 2008년 이후 전체교통사고 발생건수는 매년 감소하였다. ㄴ. 2010년 음주교통사고 발생건수는 2006년 대비 30% 이상 증가하였다. ㄷ. 전체교통사고 발생건수 중 음주교통사고 발생건수의 비중은 2010년에 가장 높았다. ㄹ. 2010년 음주교통사고의 분기별 발생건수는 3사분기(7, 8, 9월)에 가장 많았다. |
① ㄱ, ㄹ
② ㄴ, ㄷ
③ ㄴ, ㄹ
④ ㄱ, ㄴ, ㄷ
⑤ ㄱ, ㄷ, ㄹ
출처: 사이버국가고시센터
문제 해설
ㄱ. 2008년 이후 전체교통사고 발생건수는 매년 감소하였다.
(단위: 천건)
|
연 도 구 분 |
2006 | 2007 | 2008 | 2009 | 2010 |
| 전체교통사고 | 231 | 240 | 220 | 214 | 213 |
| 전년대비 증감 | – | – | – |
⇒ 2008년 이후 전체 전체교통사고 발생건수는 위 표에서 보이는 바와 같이 매년 감소했다. 따라서 보기의 내용은 옳다.
ㄴ. 2010년 음주교통사고 발생건수는 2006년 대비 30% 이상 증가하였다.
(단위: 천건)
|
연 도 구 분 |
2006 | 2007 | 2008 | 2009 | 2010 |
| 음주교통사고 | 25 | 31 | 25 | 26 | 30 |
2010년 음주교통사고 발생건수: 30건
2006년 음주교통사고 발생건수: 25건
2006년 대비 2010년 음주교통사고 발생건수 증가율 = \(\frac{30-25}{25} = \frac{5}{25}\) = 20%
2006년 대비 2010년 음주교통사고 발생건수 증가율은 20%이기 때문에 30% 이상 증가했다는 보기의 내용은 옳지 않다.
ㄷ. 전체교통사고 발생건수 중 음주교통사고 발생건수의 비중은 2010년에 가장 높았다.
(단위: 천건)
|
연 도 구 분 |
2006 | 2007 | 2008 | 2009 | 2010 |
| 전체교통사고 | 231 | 240 | 220 | 214 | 213 |
| 음주교통사고 | 25 | 31 | 25 | 26 | 30 |
| 음주교통사고 비중 |
\(\frac{25}{231}\) ≒ 11% | \(\frac{31}{240}\) ≒ 13% | \(\frac{25}{220}\) ≒ 11% | \(\frac{26}{214}\) ≒ 12% | \(\frac{30}{213}\) ≒ 14% |
전체교통사고 발생건수 중 음주교통사고 발생건수의 비중은 2010년에 14%로 전체 기간 중에서 가장 높다는 것을 위 표에서 확인할 수 있다. 따라서 보기의 내용은 옳다.
빠른 계산 팁 – 분수 크기 비교법
| \(\frac{A}{B}\)와 \(\frac{C}{D}\)에서 A > C, B > D이면 분자 간의 차와 분모 간의 차를 이용해서 두 분수의 대소를 비교할 수 있다.
\(\frac{A}{B}>\frac{A-C}{B-D}\)이면 \(\frac{A}{B}<\frac{C}{D}\)이고, \(\frac{A}{B}<\frac{A-C}{B-D}\)이면 \(\frac{A}{B}>\frac{C}{D}\)이다. 증명: \(\frac{A}{B}>\frac{A-C}{B-D}\) 식을 전개하면 \(AB-AD > AB-BC\)이다. 양변에 AB를 소거하면 \(-AD > -BC\)이 된다. 또 양변에 -1을 곱하게 되면 부호가 바뀌어 \(AD < BC\)가 된다. 다시 여기에 양변에 BD로 나누게 되면 \(\frac{A}{B}<\frac{C}{D}\)이 된다. 예) $$ |
이를 이용해서 분수의 크기를 비교한다.
분수는 분자가 클수록 분모가 작을수록 그 값이 커진다.
(단위: 천건)
|
연 도 구 분 |
2006 | 2007 | 2008 | 2009 | 2010 |
| 전체교통사고 | 231 | 240 | 220 | 214 | 213 |
| 음주교통사고 | 25 | 31 | 25 | 26 | 30 |
전체 기간 중에 분자에 해당하는 음주교통사고 건수가 제일 높은 해는 2007년 31건이다. 또한 분모에 해당하는 전체교통사고 건수가 제일 낮은 해는 2010년 213건이다.
2007년과 2010년의 전체교통사고 발생건수 중 음주교통사고 발생건수의 비중을 나타내면
$$\frac{31}{240}, \frac{30}{213}$$
이다.
두 분수의 분자와 분모 간의 차는 \(\frac{1}{27}=\frac{31-30}{240-213}\)이 되고, 이를 통분하면 \(\frac{9}{243}=\frac{1×9}{27×9}\)가 된다.
\(\frac{31}{240}\text{와 } \frac{9}{243}\)를 비교하면 분자가 더 크고 분모가 더 작은 \(\frac{31}{240}\)이 확실히 더 크다.
$$
\begin{align}
\frac{31}{240}&>\frac{9}{243}\\
∴ \frac{31}{240}\text{(2007년)}&<\frac{30}{213}\text{(2010년)}\\
\end{align}
$$
따라서 2010년의 음주교통사고 발생건수의 비중이 제일 높다.
ㄹ. 2010년 음주교통사고의 분기별 발생건수는 3사분기(7, 8, 9월)에 가장 많았다.
<그림> 2010년 교통사고 발생건수의 월별 구성비

그림에 표시된 월별 구성비는 2010년 전체 음주교통사고 발생건수 대비 해당 월 음주교통사고 발생건수의 비중을 나타낸다. 따라서 각 분기에 해당하는 구성비의 합이 클수록 음주교통사고 발생건수가 높다.
| 분기 | 구성비의 합 |
| 1사분기 | 6.7 + 6.3 + 7.4 = 20.4% |
| 2사분기 | 8.0 + 8.3 + 7.9 = 24.2% |
| 3사분기 | 10.1 + 8.5 + 9.4 = 28.0% |
| 4사분기 | 9.4 + 10.1 + 7.9 = 26.4% |
3사분기의 구성비의 합이 28.0%로 전체 분기 중에서 가장 높다. 따라서 보기의 내용은 옳다.
빠른 계산 팁
그림에서 분기별 그래프 추세를 보면 3사분기와 4사분기가 나머지 분기보다 높다는 것을 확인할 수 있다.
3사분기와 4사분기의 구성비를 보면 10.1%, 9.4%가 공통적으로 있고 8.5%, 7.9%가 있다. 8.5%가 7.9%보다는 높기 때문에 3사분기의 음주교통사고 발생건수가 더 많다는 것을 알 수 있다.
정답은 ⑤번이다.
2011 민경채 PSAT 자료해석
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 25번 (월별 상품 판매고 단순이동평균 계산 팁)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 24번 (의약품 특허출원 다국적기업 다이어트제)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 23번 (식품사업부 외식사업부 전입 전출)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 22번 (지역별 영유아 인구수 보육시설 정원)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 21번 (외국인 소유 토지면적 분수 대소 비교)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 20번 (경제 전망 보고서 실업률 경제 성장률 소비자물가)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 19번 (국민은행 총자산 당기순이익 그래프)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 18번 (교통사고 발생건수 분수 대소 비교)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 17번 (양성평등정책)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 16번 (친환경 농산물 생산량)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 15번 (회원기금원금 회원급여저축총액)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 14번 (정부지원 직업훈련 실업자 재직자 지원금 분수 대소 비교)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 13번 (암 발생률 그래프 분석)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 12번 (사채발행차금 사채 이자비용 액면이자)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 11번 (TV 프로그램 시청률 45도선 보조선)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 10번 (석유수요 중국 인도 중동 남미)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 9번 (세계 에너지 수요 보고서 자료 이용)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 8번 (외식업체 공급업체 선호도)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 7번 (공익근무요원 분수 대소 비교)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 6번 (은행 영업수익 이자수익)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 5번 (외국인 입국자 수 그래프 보고서 자료 이용)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 4번 (조피볼락 분수 대소 비교)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 3번 (소득탄력성 소득 구매량)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 2번 (약물 완치 환자수)
- [PSAT 기출] 2011 5급 민경채 자료해석 력책형 1번 해설 (지식산업센터 개별입지)
관련 문서
- 2011 민경채 PSAT 해설 모음
- 5급 PSAT 자료해석 해설 모음
- 5급 PSAT 해설 모음
- 국가직 7급 PSAT 자료해석 해설 모음
- 국가직 7급 PSAT 해설 모음
- 민경채 PSAT 자료해석 해설 모음
- 민경채 PSAT 해설 모음
- PSAT 기출 해설 모음
- PSAT 명제 논리 문제 해설 모음
- PSAT 정언 논리 문제 해설 모음
- 정언 논리 공부 자료
- PSAT 추론 문제 해설 모음
- PSAT 강화 약화 문제 해설 모음
- PSAT 법조문 문제 해설 모음
- PSAT 논리퀴즈 문제 해설 모음


