[PSAT 기출] 2013 외교관후보자 선발 상황판단 인책형 37번 해설 – 삼각형 무게중심 좌표계

개요

다음은 2013년 국가공무원 외교관후보자 선발 PSAT 상황판단영역 인책형 37번 문제 해설이다.

문 37. 다음 <조건>을 근거로 판단할 때, <보기>에서 옳은 것을 모두 고르면?

<조 건>

삼각형의 내부(각 꼭지점과 각 변 포함)의 한 점을 표시할 때, 세 개의 좌표축을 사용하는 무게중심 좌표계는 다음과 같이 정의된다.

1. 위 삼각형에서 내부의 한 점 P를 잡았을 때, △PBC, △PCA, △PAB의 면적이 차례대로 X, Y, Z인 경우, 좌표값을 x＝X/(X＋Y＋Z), y＝Y/(X＋Y＋Z), z＝Z/(X＋Y＋Z)로 정의하여 P(x, y, z)와 같이 내부의 점을 표시한다.

2. 삼각형의 각 꼭지점은 무게중심 좌표계로 나타냈을 때, A(1, 0, 0), B(0, 1, 0) 그리고 C(0, 0, 1)로 표시된다.

※ 삼각형의 무게중심에서 삼각형의 꼭지점을 연결해서 만들어지는 세 삼각형의 면적은 모두 같다.

<보 기>

ㄱ. △ABC의 세 변 AB, BC, CA 위에 존재하는 점 중에서 꼭지점 A, B, C를 제외한 나머지 점을 무게중심 좌표계로 나타냈을 때, 좌표값 중 한 개는 반드시 0이다.

ㄴ. 각 꼭지점과 각 변에 존재하는 점을 제외한 삼각형 내부의 점을 무게중심 좌표계로 나타냈을 때, 각 좌표값 x, y, z는 0과 1 사이의 정수로 표시된다.

ㄷ. 삼각형의 무게중심을 G라 하고, 이를 무게중심 좌표계로 나타내면 G(1/3, 1/3, 1/3)로 표시된다.

ㄹ. △ABC의 내부에 변 BC와 평행한 임의의 선분을 표시한다. 그 선분 위에 존재하는 점 P1, P2를 무게중심 좌표계로 나타내면, 각각 P1(x₁, y₁, z₁), P2(x₂, y₂, z₂)로 표시되고, 좌표값 x₁과 x₂는 항상 동일하다.

① ㄱ, ㄷ

② ㄱ, ㄹ

③ ㄷ, ㄹ

④ ㄱ, ㄷ, ㄹ

⑤ ㄴ, ㄷ, ㄹ

출처: 사이버국가고시센터

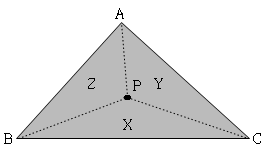P(x, y, z)의 각 좌표값은 전체 삼각형 △ABC 면적에 대한 작은 삼각형 면적의 비율이다.

만약 P가 변 BC에 있다면 △PBC, 즉 X의 값은 0이 된다.

그러므로 P가 꼭지점을 제외한 △ABC의 세 변 AB, BC, CA 위에 존재하는 어느 점 위에 있다면 좌표계 중 한 개는 반드시 0이다.

따라서 보기의 내용은 옳다.

ㄴ. 각 꼭지점과 각 변에 존재하는 점을 제외한 삼각형 내부의 점을 무게중심 좌표계로 나타냈을 때, 각 좌표값 x, y, z는 0과 1 사이의 정수로 표시된다.

P(x, y, z)의 각 좌표값은 전체 삼각형 △ABC 면적에 대한 작은 삼각형 면적의 비율이다.

만약 P(x, y, z)가 삼각형의 무게중심에 있을 때, △PBC, △PCA, △PAB의 면적은 모두 같게 되고, 그렇다면 P(x, y, z)은 P(1/3, 1/3, 1/3)가 된다.

\(\dfrac{\text{1}}{\text{3}}\) = 0.333….은 정수가 아니라 무한소수이다.

따라서 보기의 내용은 옳지 않다.

ㄷ. 삼각형의 무게중심을 G라 하고, 이를 무게중심 좌표계로 나타내면 G(1/3, 1/3, 1/3)로 표시된다.

P(x, y, z)의 각 좌표값은 전체 삼각형 △ABC 면적에 대한 작은 삼각형 면적의 비율이다.

P(x, y, z)가 삼각형의 무게중심에 있을 때, △PBC, △PCA, △PAB의 면적은 모두 같게 되고, 그렇다면 P(x, y, z)은 G(1/3, 1/3, 1/3)가 된다.

보기의 내용은 옳다.

ㄹ. ㄹ. △ABC의 내부에 변 BC와 평행한 임의의 선분을 표시한다. 그 선분 위에 존재하는 점 P1, P2를 무게중심 좌표계로 나타내면, 각각 P1(x₁, y₁, z₁), P2(x₂, y₂, z₂)로 표시되고, 좌표값 x₁과 x₂는 항상 동일하다.

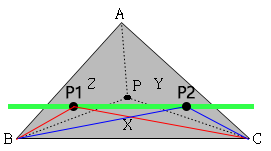밑변의 길이는 BC로 같고 높이도 같기 때문에 삼각형 X₁과 X₂의 면적은 같다.

P(x, y, z)의 각 좌표값은 전체 삼각형 △ABC 면적에 대한 작은 삼각형 면적의 비율이다.

그러므로 좌표값 x₁과 x₂는 항상 동일하다.

따라서 보기의 내용은 옳다.

정답은 ④번이다.