[PSAT 기출] 2013 5급 언어논리 인책형 39번 40번 해설 – 관찰 사례 명제 α 규칙

1 개요
2 문제
3 39번 문제 해설
4 40번 문제 해설
5 2013 5급 PSAT 언어논리
6 관련 문서

개요

다음은 2013년 국가공무원 5급 언어논리영역 인책형 39번, 40번 문제 해설이다.

문제

※ 다음 글을 읽고 물음에 답하시오. [문 39~문 40]

어떤 관찰 사례를 토대로 “모든 A는 B의 속성을 지녔다.”라는 명제가 입증되었다고 하자. 이 경우 그 관찰 사례는 “모든 A는 B의 속성을 지녔다.”라는 명제를 논리적으로 함축하는 다른 명제에 대해서는 어떤 관계를 지니는가? 어떤 명제가 다른 명제를 함축한다는 것은 앞의 명제가 참일 경우 뒤의 명제도 반드시 참이라는 것을 뜻한다. 과학적 명제들은 커다란 체계 안에서 논리적으로 서로 연관되어 있다고 보는 것이 타당하고, 한 사례가 단 하나의 명제에 대해서만 입증력을 갖는다고 볼 이유는 없다. 여기서 “모든 C는 B의 속성을 지닌다.”라는 명제를 생각해보자. 만일 C가 A의 부분집합에 해당한다면, 앞서 언급한 그 관찰 사례는 “모든 C는 B의 속성을 지녔다.”라는 명제 역시 입증할 것이라고 보는 것이 우리의 직관과 부합한다. 즉, 한 관찰 사례가 어떤 명제를 입증할 경우 그 사례는 그 명제가 논리적으로 함축하는 임의의 명제도 입증한다는 것이다. 이를 α 규칙이라고 부르자.

한편, A를 부분집합으로 갖는 집합 D에 대해서는 어떨까? 앞서 서술한 그 관찰의 사례는 “모든 D는 B의 속성을 지녔다.”라는 명제를 입증할 것인가? 적잖은 이들이 이 물음에 대해서도 긍정의 대답을 제시한다. 예컨대 실험이나 관찰에 의해 “모든 구리는 도체다.”라는 명제가 입증되었다면 “모든 금속은 도체다.”라는 명제도 긍정적으로 평가되어야 한다는 생각이다. 이 경우를 일반화하여 말하면, 한 관찰 사례가 어떤 명제를 입증할 경우 그 사례는 그 명제를 논리적으로 함축하는 임의의 명제도 입증하리라고 생각할 수 있다. 이를 β 규칙이라고 부르자.

한 사례가 서로 연관된 두 명제에 대해 지니는 의미를 규정하는 위의 두 규칙은 모두 직관적 호소력을 지닌다. 그런데 문제는 α 규칙과 β 규칙을 모두 인정할 경우 곤혹스런 결론이 우리를 기다린다는 사실이다. 어떤 관찰 사례에 의해 어떤 명제 P가 입증되었다고 하자. 이 관찰 사례는 ㉠ 에 의거하여 ㉡ 라는 명제를 입증할 것이다. 이 명제에 포함되어 있는 Q가 어떤 내용인지는 아무런 상관이 없다. 왜냐하면 이 명제가 참일 경우 명제 P 역시 참일 수밖에 없다는 의미에서 이 명제는 P를 논리적으로 함축하고, 이렇게 판단하는 데에 Q가 어떤 내용의 명제인가는 고려되지 않기 때문이다. 이번에는 이 명제에 ㉢ 을 적용해보자. 그러면 우리는 문제의 관찰 사례가 명제 Q도 입증한다고 평가하게 된다. 그런데 이미 강조했듯이 우리는 명제 Q의 내용에 대해 아무런 제약도 요구한 바 없다. 문제의 관찰 사례는 이제 임의의 명제 Q를 입증하게 된 셈이다. 물론 이것은 말도 안 되는 상황이다. 이렇게 해서 일견 합리적인 두 가지 규칙 α와 β 가운데 적어도 하나는 수용하기 어렵다는 결론에 도달하게 된다.

문 39. 위 글의 ㉠∼㉢에 들어갈 말을 바르게 나열한 것은?

	㉠	㉡	㉢
①	α 규칙	“P이고 Q이다.”	β 규칙
②	α 규칙	“P이지만 Q는 아니다.”	β 규칙
③	α 규칙	“Q이면 P이다.”	β 규칙
④	β 규칙	“P이고 Q이다.”	α 규칙
⑤	β 규칙	“P이지만 Q는 아니다.”	α 규칙

문 40. 위 글에서 추론할 수 없는 것은?

① α 규칙을 적용하면, “모든 A는 B의 속성을 지녔다.”라는 명제를 입증하는 사례는, “모든 A는 B의 속성을 지녔다.”라는 명제가 함축하는 모든 명제를 입증할 수 있다.

② β 규칙을 적용하면, “모든 A는 B의 속성을 지녔다.”라는 명제를 입증하는 사례는, “모든 A는 B의 속성을 지녔다.”라는 명제가 함축하지 않는 어떤 명제를 입증할 수 있다.

③ α 규칙을 적용하면, “모든 A는 B의 속성을 지녔다.”라는 명제를 입증하는 사례는, A를 부분집합으로 갖는 집합 S에 관한 모든 명제를 입증할 수 있다.

④ β 규칙을 적용하면, “모든 A는 B의 속성을 지녔다.”라는 명제를 입증하는 사례는, A를 부분집합으로 갖는 집합 S에 관한 어떤 명제를 입증할 수 있다.

⑤ α 규칙과 규칙을 모두 적용하면, “모든 A는 B의 속성을 지녔다.”라는 명제를 입증하는 사례는, A를 부분집합으로 갖는 집합 S에 관한 어떤 명제를 입증할 수 있다.

출처: 사이버국가고시센터

39번 문제 해설

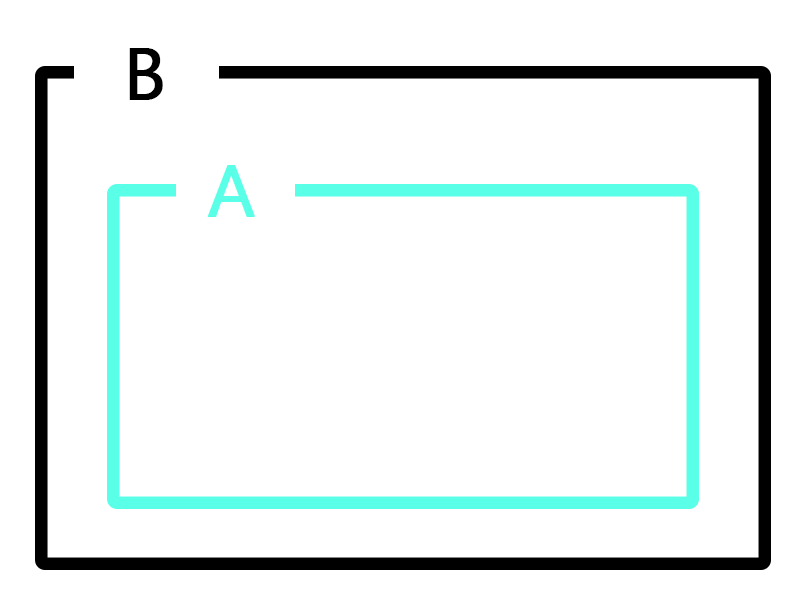“모든 A는 B의 속성을 지녔다.”

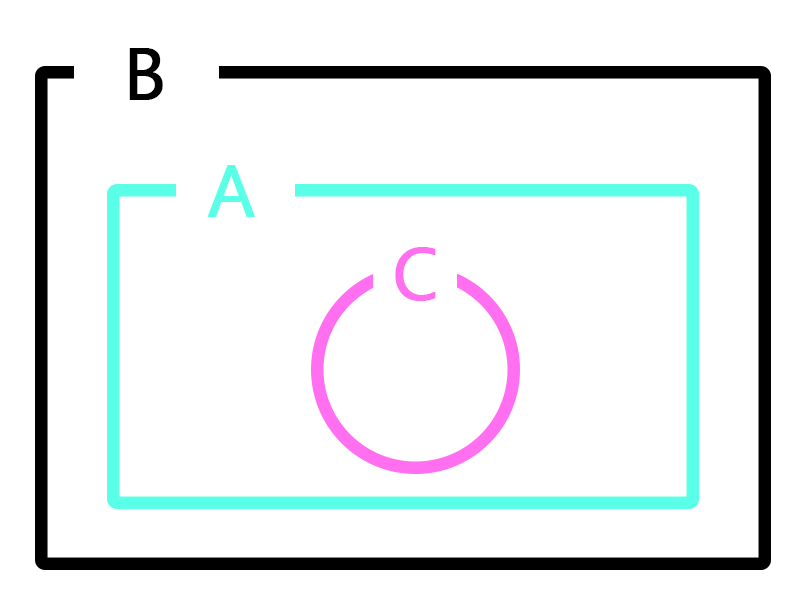만일 C가 A의 부분집합에 해당한다면, 앞서 언급한 그 관찰 사례는 “모든 C는 B의 속성을 지녔다.”라는 명제 역시 입증할 것이라고 보는 것이 우리의 직관과 부합한다.

한 관찰 사례가 어떤 명제를 입증할 경우 그 사례는 그 명제가 논리적으로 함축하는 임의의 명제도 입증한다는 것이다. 이를 α 규칙이라고 부르자.

< α 규칙>

“모든 A는 B의 속성을 지녔다.”	참
↓ 함축 ↓ 입증
“모든 C는 B의 속성을 지녔다.”	참

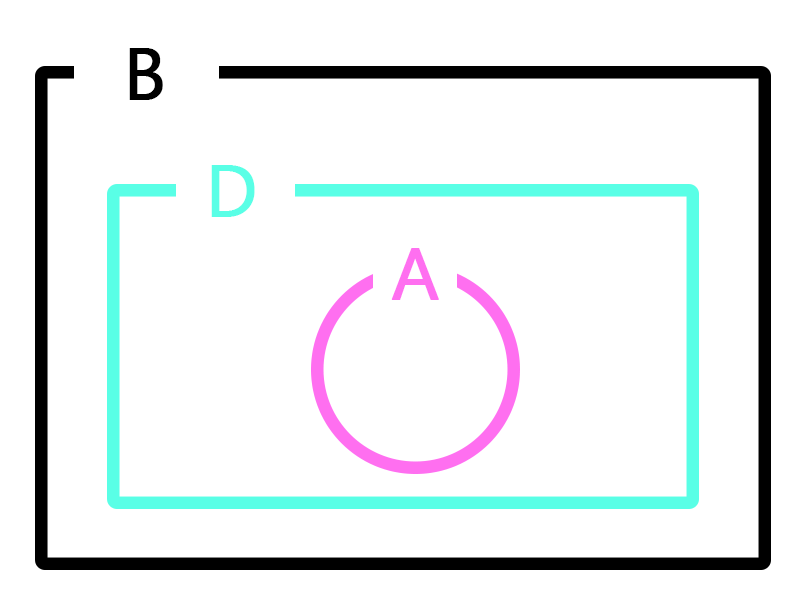A를 부분집합으로 갖는 집합 D에 대해서는 어떨까? 앞서 서술한 그 관찰의 사례는 “모든 D는 B의 속성을 지녔다.”라는 명제를 입증할 수 있을까?

한 관찰 사례가 어떤 명제를 입증할 경우 그 사례는 그 명제를 논리적으로 함축하는 임의의 명제도 입증하리라고 생각할 수 있다. 이를 β 규칙이라고 부르자.

< β 규칙>

“모든 D는 B의 속성을 지녔다.”	참
↓ 함축 ↑ 입증
“모든 A는 B의 속성을 지녔다.”	참

어떤 관찰 사례에 의해 어떤 명제 P가 입증되었다고 하자. 이 관찰 사례는 ㉠ 에 의거하여 ㉡ 라는 명제를 입증할 것이다. 이 명제에 포함되어 있는 Q가 어떤 내용인지는 아무런 상관이 없다. 왜냐하면 이 명제가 참일 경우 명제 P 역시 참일 수밖에 없다는 의미에서 이 명제는 P를 논리적으로 함축하고, 이렇게 판단하는 데에 Q가 어떤 내용의 명제인가는 고려되지 않기 때문이다.

< β 규칙>

“P이고 Q이다.” 또는 “P이지만 Q는 아니다.”	참
↓ 함축 ↑ 입증
명제 P	참

㉠에 들어갈 말은 β 규칙이다.

㉡에 들어갈 말은 아직 알 수 없다.

이번에는 이 명제에 ㉢ 을 적용해보자. 그러면 우리는 문제의 관찰 사례가 명제 Q도 입증한다고 평가하게 된다. 그런데 이미 강조했듯이 우리는 명제 Q의 내용에 대해 아무런 제약도 요구한 바 없다. 문제의 관찰 사례는 이제 임의의 명제 Q를 입증하게 된 셈이다. 물론 이것은 말도 안 되는 상황이다. 이렇게 해서 일견 합리적인 두 가지 규칙 α와 β 가운데 적어도 하나는 수용하기 어렵다는 결론에 도달하게 된다.

< α 규칙>

“P이고 Q이다.” 또는 ~~“P이지만 Q는 아니다.”~~	참
↓ 함축 ↓ 입증
명제 Q	참

β 규칙에 따라 “P이고 Q이다.”라는 명제가 입증되었다. “P이고 Q이다.”는 명제 논리 기호로 P∧Q로 나타낼 수 있으며, P와 Q 모두 참이라는 뜻이다.

α 규칙에 따라 “P이고 Q이다.(P∧Q)”라는 명제를 통해 명제 Q가 입증된다. 하지만 “P이지만 Q는 아니다.”라는 명제를 통해서 명제 Q가 입증될 수 없다. Q는 아니라는 것은 거짓이라는 뜻이기 때문이다.

문제는 처음에 β 규칙에 따라 “P이고 Q이다.”라는 명제를 입증했을 때, Q가 어떤 내용인지 고려를 하지 않고 아무런 제약 없이 입증되었기 때문에 진짜 명제 Q가 참이라고 할 수 없다는 점이다.

문제의 관찰 사례는 이제 임의의 명제 Q를 입증하게 된 셈이다. 물론 이것은 말도 안 되는 상황이다. 이렇게 해서 일견 합리적인 두 가지 규칙 α와 β 가운데 적어도 하나는 수용하기 어렵다는 결론에 도달하게 된다.

정답은 ④번이다.

40번 문제 해설

따라서 보기의 내용은 옳다.

“모든 A는 B의 속성을 지녔다.”라는 명제는 “모든 D는 B의 속성을 지녔다.”는 명제를 함축하지 않는다.

α 규칙을 적용하면, “모든 D는 B의 속성을 지녔다.”는 명제를 입증할 수 없지만, β 규칙을 적용하면, 이 명제를 입증할 수 있다.

따라서 보기의 내용은 옳다.

A를 부분집합으로 갖는 집합 D에 관한 명제처럼, β 규칙을 적용하면, 입증이 가능하지만, α 규칙을 적용하면, 입증이 불가능하다.

따라서 보기의 내용은 옳지 않다.

A를 부분집합으로 갖는 집합 D에 관한 명제처럼, β 규칙을 적용하면, 입증이 가능하다.

따라서 보기의 내용은 옳다.

⑤ α 규칙과 β 규칙을 모두 적용하면, “모든 A는 B의 속성을 지녔다.”라는 명제를 입증하는 사례는, A를 부분집합으로 갖는 집합 S에 관한 어떤 명제를 입증할 수 있다.

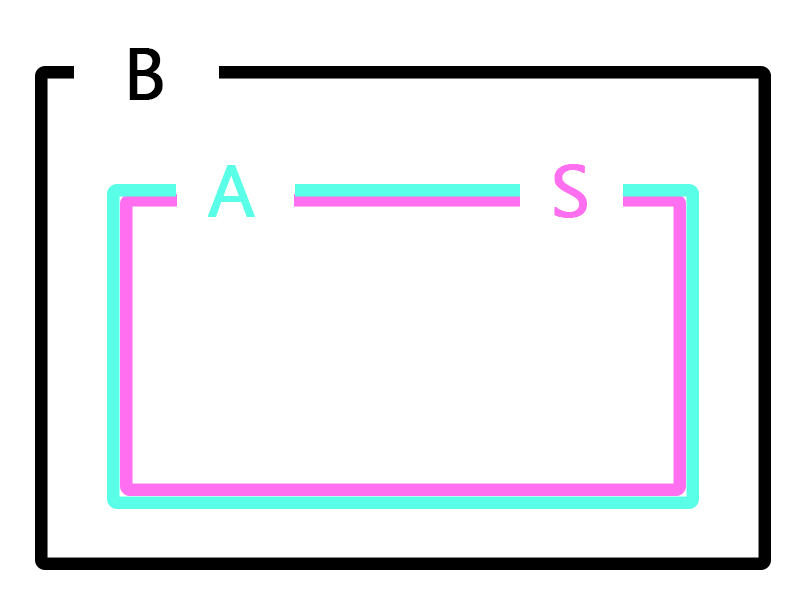A와 S가 동치라면, 서로가 서로에 대하여 부분집합이 될 수 있다.

< α 규칙>

“모든 A는 B의 속성을 지녔다.”	참
↓ 함축 ↓ 입증
“모든 S는 B의 속성을 지녔다.”	참

< β 규칙>

“모든 S는 B의 속성을 지녔다.”	참
↓ 함축 ↑ 입증
“모든 A는 B의 속성을 지녔다.”	참

α 규칙과 β 규칙을 모두 적용하면, 위와 같은 명제를 입증할 수 있다.

따라서 보기의 내용은 옳다.

정답은 ③번이다.

개요

문제

39번 문제 해설

40번 문제 해설

2013 5급 PSAT 언어논리

관련 문서

답글 남기기 응답 취소