[PSAT 기출] 2015 민경채 상황판단 인책형 8번 해설 – 씨름대회 대진표 추첨 확률 논리퀴즈

개요

다음은 2015년 국가공무원 민간경력자 일괄채용 (민경채) 상황판단영역 인책형 8번 문제 해설이다.

문 8. 다음 <규칙>을 근거로 판단할 때, <보기>에서 옳은 것만을 모두 고르면?

<규 칙>

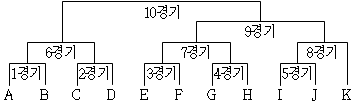
○ △△배 씨름대회는 아래와 같은 대진표에 따라 진행되며, 11명의 참가자는 추첨을 통해 동일한 확률로 A부터 K까지의 자리 중에서 하나를 배정받아 대회에 참가한다.

○ 대회는 첫째 날에 1경기부터 시작되어 10경기까지 순서대로 매일 하루에 한 경기씩 쉬는 날 없이 진행되며, 매 경기에서는 무승부 없이 승자와 패자가 가려진다.

○ 각 경기를 거듭할 때마다 패자는 제외시키면서 승자끼리 겨루어 최후에 남은 두 참가자 간에 우승을 가리는 승자 진출전 방식으로 대회를 진행한다.

<보 기>

ㄱ. 이틀 연속 경기를 하지 않으면서 최소한의 경기로 우승할 수 있는 자리는 총 5개이다.

ㄴ. 첫 번째 경기에 승리한 경우 두 번째 경기 전까지 3일 이상을 경기 없이 쉴 수 있는 자리에 배정될 확률은 50% 미만이다.

ㄷ. 총 4번의 경기를 치러야 우승할 수 있는 자리에 배정될 확률이 총 3번의 경기를 치르고 우승할 수 있는 자리에 배정될 확률보다 높다.

① ㄱ

② ㄴ

③ ㄷ

④ ㄱ, ㄷ

⑤ ㄴ, ㄷ

출처: 사이버국가고시센터

ㄱ. 이틀 연속 경기를 하지 않으면서 최소한의 경기로 우승할 수 있는 자리는 총 5개이다.

매일 하루에 한 경기씩 쉬는 날 없이 경기가 치러진다.

그렇다면 이틀 연속으로 경기를 한다면 당일 경기와 다음날 경기와의 차이가 1경기가 날 것이다. 예를 들어 위 그림에서 8경기와 9경기와의 경기 일수 차이가 하루가 되어 이틀 연속으로 경기를 한다.

또한 이틀 연속 경기를 하지 않으면서 최소한의 경기로 우승할 수 있는 경기는 총 3경기이다. 예를 들어 A의 경우 3연승을 한다면 우승할 수 있다.

이틀 연속 경기를 하지 않으면서 최소한의 경기인 3경기로 우승할 수 있는 자리는 A, B, C, D 총 4개이다. E, F, G, H는 총 4경기, I, J, K는 이틀 연속으로 경기를 해야 한다.

따라서 보기의 내용은 옳지 않다.

ㄴ. 첫 번째 경기에 승리한 경우 두 번째 경기 전까지 3일 이상을 경기 없이 쉴 수 있는 자리에 배정될 확률은 50% 미만이다.

첫 번째 경기와 두 번째 경기와의 경기 수 차이가 3경기 이상 나는 자리를 찾는다. A, B, C, D, E, F, G, H, I, J이다.

첫 번째 경기에 승리한 경우 두 번째 경기 전까지 3일 이상을 경기 없이 쉴 수 있는 자리에 배정될 확률은 10/11 ≒ 90.9%이다.

따라서 보기의 내용은 옳지 않다.

ㄷ. 총 4번의 경기를 치러야 우승할 수 있는 자리에 배정될 확률이 총 3번의 경기를 치르고 우승할 수 있는 자리에 배정될 확률보다 높다.

총 4번의 경기를 치러야 우승할 수 있는 자리는 E, F, G, H, I, J 총 6개이다.

총 3번의 경기를 치러야 우승할 수 있는 자리는 A, B, C, D, J 총 5개이다.

따라서 보기의 내용은 옳다.

정답은 ③번이다.