문제
10. 다음 글의 빈칸에 들어갈 내용으로 가장 적절한 것은?
| 갑은 이번에 들어온 신입 사원 민철에 대해서 ‘그는 결혼하지 않았다.’라는 정보와 ‘그는 비혼이다.’라는 정보를 획득했다. 한편 을은 민철에 대해서 ‘그는 결혼하지 않았다.’라는 정보와 ‘그에게는 아이가 있다.’라는 정보를 획득했다. 갑이 획득한 정보 집합과 을이 획득한 정보 집합 중에서 무엇이 더 정합적인가? 다르게 말해 어떤 집합 내 정보들이 서로 더 잘 들어맞는가? 갑의 정보 집합이 더 정합적이라고 여기는 것이 상식적이다.
그렇다면 이런 정보 집합의 정합성은 어떻게 측정할 수 있을까? 그 방법 중 하나인 C는 확률을 이용해 그 정합성의 정도, 즉 정합도를 측정한다. 여러 정보로 이루어진 정보 집합 S가 있다고 해보자. 방법 C에 따르면, S의 정합도는 그 정의에 따라 정합도를 측정하면, 위 갑과 을이 획득한 정보 집합의 정합성을 우리의 상식에 맞춰 비교할 수 있다. 갑이 획득한 정보에서 ‘그가 결혼하지 않았으며 비혼일 확률’과 ‘그가 결혼하지 않았거나 비혼일 확률’은 모두 ‘그가 비혼일 확률’과 같다. 왜냐하면 결혼하지 않았다는 것과 비혼이라는 것은 서로 같은 말이기 때문이다. 따라서 방법 C에 따르면 갑이 획득한 정보 집합의 정합도는 1이다. 한편, ‘그가 결혼하지 않았으며 아이가 있을 확률’은 ‘그가 결혼하지 않았거나 아이가 있을 확률’보다 낮다. 왜냐하면 그가 결혼하지 않았거나 아이가 있는 경우에 비해, 그가 결혼하지 않고 아이가 있는 경우는 드물기 때문이다. 따라서 방법 C에 따르면 을의 정보 집합의 정합도는 1보다 작다. 이런 식으로 방법 C는 갑의 정보 집합의 정합도가 을의 정보 집합의 정합도보다 크다고 말해 준다. 그리고 그 점에서 갑의 정보 집합이 을의 정보 집합보다 더 정합적이라고 판단한다. 이는 우리 상식에 부합하는 결과이다. |
① S의 정보 중 적어도 하나가 참일 확률을 S의 모든 정보가 참일 확률로 나눈 값
② S의 모든 정보가 참일 확률을 S의 정보 중 적어도 하나가 참일 확률로 나눈 값
③ S의 정보 중 기껏해야 하나가 참일 확률을 S의 모든 정보가 참일 확률로 나눈 값
④ S의 모든 정보가 참일 확률을 S의 정보 중 기껏해야 하나가 참일 확률로 나눈 값
⑤ S의 정보 중 기껏해야 하나가 참일 확률을 S의 정보 중 적어도 하나가 참일 확률로 나눈 값
출처: 사이버국가고시센터
문제 해설
① S의 정보 중 적어도 하나가 참일 확률을 S의 모든 정보가 참일 확률로 나눈 값
 |
갑의 정보 집합의 정합도 = \(\dfrac{\text{A}}{\text{A}}\) = 1
을의 정보 집합의 정합도 = \(\dfrac{\text{X+Q+W}}{\text{Q}}\) > 1
갑의 S의 정보 중 적어도 하나가 참일 확률 = 그가 결혼하지 않았거나 비혼일 확률(A)
갑의 S의 모든 정보가 참일 확률 = 그가 결혼하지 않았으며 비혼일 확률(A)
보기의 경우 갑의 정보 집합의 정합도는 1이다. 갑의 입장에서 ‘그가 결혼하지 않았으며 비혼일 확률(A)’과 ‘그가 결혼하지 않았거나 비혼일 확률(A)’은 모두 ‘그가 비혼일 확률(A)’로 같다.
을의 S의 정보 중 적어도 하나가 참일 확률 = 그가 결혼하지 않았거나 아이가 있을 확률(X+Q+W)
을의 S의 모든 정보가 참일 확률 = 그가 결혼하지 않았으며 아이가 있을 확률(Q)
하지만 을의 정보 집합의 정합도는 1을 넘는다. 을 입장에서 ‘그가 결혼하지 않았으며 아이가 있을 확률(Q)’은 ‘그가 결혼하지 않았거나 아이가 있을 확률(X+Q+W)’보다 낮기 때문이다.
따라서 보기의 내용은 옳지 않다.
② S의 모든 정보가 참일 확률을 S의 정보 중 적어도 하나가 참일 확률로 나눈 값
 |
갑의 정보 집합의 정합도 = \(\dfrac{\text{A}}{\text{A}}\) = 1
을의 정보 집합의 정합도 = \(\dfrac{\text{Q}}{\text{X+Q+W}}\) < 1
을의 S의 모든 정보가 참일 확률 = 그가 결혼하지 않았으며 아이가 있을 확률(Q)
을의 S의 정보 중 적어도 하나가 참일 확률 = 그가 결혼하지 않았거나 아이가 있을 확률(X+Q+W)
을의 정보 집합의 정합도는 1보다 작다. 을 입장에서 ‘그가 결혼하지 않았으며 아이가 있을 확률(Q)’은 ‘그가 결혼하지 않았거나 아이가 있을 확률(X+Q+W)’보다 낮기 때문이다.
따라서 보기의 내용은 옳다.
③ S의 정보 중 기껏해야 하나가 참일 확률을 S의 모든 정보가 참일 확률로 나눈 값
 |
갑의 정보 집합의 정합도 = \(\dfrac{\text{0}}{\text{A}}\) = 0
을의 정보 집합의 정합도 = \(\dfrac{\text{X+W}}{\text{Q}}\) >< 1 ??
S의 정보 중 기껏해야 하나가 참일 확률은 전체에서 S의 정보 중 많아봤자 하나만 참인 경우를 말한다. 즉 교집합을 제외한 나머지이다.
보기의 경우 갑의 정보 집합의 정합도는 0이다. 갑의 입장에서 ‘그가 결혼하지 않았다’와 ‘그는 비혼이다’는 같기 때문에 ‘그가 결혼하지 않았다’ 또는 ‘그는 비혼이다’ 중 하나만 참일 확률은 0이 된다.
하지만 을의 정보 집합의 정합도는 알 수 없다. 을 입장에서 ‘그는 결혼하지 않았다’와 ‘아이가 있다’ 중 하나만 참일 확률(X+W)을 알 수 없기 때문에, 이 확률이 ‘그가 결혼하지 않았으며 아이가 있을 확률(Q)’보다 큰지 작은지 알 수 없다.
따라서 보기의 내용은 옳지 않다.
④ S의 모든 정보가 참일 확률을 S의 정보 중 기껏해야 하나가 참일 확률로 나눈 값
 |
갑의 정보 집합의 정합도 = \(\dfrac{\text{A}}{\text{0}}\) = ??
을의 정보 집합의 정합도 = \(\dfrac{\text{Q}}{\text{X+W}}\) >< 1 ??
따라서 보기의 내용은 옳지 않다.
⑤ S의 정보 중 기껏해야 하나가 참일 확률을 S의 정보 중 적어도 하나가 참일 확률로 나눈 값
 |
갑의 정보 집합의 정합도 = \(\dfrac{\text{0}}{\text{A}}\) = 0
을의 정보 집합의 정합도 = \(\dfrac{\text{X+W}}{\text{X+Q+W}}\) < 1
따라서 보기의 내용은 옳지 않다.
정답은 ②번이다.
2024 국가직 7급 PSAT 언어논리
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 25번 해설 – 논쟁 K국 형법 이중처벌 금지의 원칙
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 24번 해설 – 주민등록 출산장려금
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 23번 해설 – 보호수준 평가 취약기관 우수기관
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 22번 해설 – 주류 판매 추론
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 21번 해설 – 아동학대 보호조치
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 19번 20번 해설 – 명제 P 인식적 정당화 명제 논리
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 18번 해설 – 광검출기 광포화점 암전류
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 17번 해설 – 나노 구조체 전자 방출 강화 약화
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 16번 해설 – 근육 세포 수축 이완 아세틸콜린 추론
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 15번 해설 – 절연체 전하 추론
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 14번 해설 – 문 주무관 문공 팀 명제 논리
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 13번 해설 – 가훈 구슬치기 명제논리 논리퀴즈
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 12번 해설 – 프로젝트 주무관 명제논리 논리퀴즈
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 11번 해설 – 지각적 경험 신의 마음 명제 논리
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 10번 해설 – 정보 집합 정합적 정합도 확률
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 9번 해설 – 뇌 전측대상피질 ACC
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 8번 해설 – 좋아요 콘텐츠
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 7번 해설 – 논어 자한 공자 인 문맥 수정
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 6번 해설 – 과학자 이론 과학적 진보
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 5번 해설 – 인두법 우두법
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 4번 해설 – 필사문화 공동체적 독서 전근대
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 3번 해설 – 헌법 국민 인민 유진오
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 2번 해설 – 사고 포쇄 겸직사관
- [PSAT 기출] 2024 국가직 7급 언어논리 사책형 1번 해설 – 고종 전차 한성전기회사
관련 문서
- 2024 7급 PSAT 해설 모음
- 5급 PSAT 언어논리 해설 모음
- 5급 PSAT 해설 모음
- 국가직 7급 PSAT 언어논리 해설 모음
- 국가직 7급 PSAT 해설 모음
- 민경채 PSAT 언어논리 해설 모음
- 민경채 PSAT 해설 모음
- PSAT 기출 해설 모음
- PSAT 명제 논리 문제 해설 모음
- PSAT 정언 논리 문제 해설 모음
- 정언 논리 공부 자료
- PSAT 추론 문제 해설 모음
- PSAT 강화 약화 문제 해설 모음
- PSAT 법조문 문제 해설 모음
- PSAT 논리퀴즈 문제 해설 모음


이런 문제에 대한 접근이 쉽지 않은데ㅡ
이런 류는 어떤 책을 참고로 배경을 쌓아두면 좋은지
혹시 추천해주실 수 있나요?
글쎄요…
일단 시중에 나와 있는 PSAT 기본서를 반복해서 회독하는 것을 추천드립니다. 많을수록 좋지만 최소 3번을 돌리시면 어느 정도 문제를 보는 시야가 넓어질 것입니다.
그러고 나서 이와 같은 기출문제를 반복해서 푸는 것입니다.
너무 뻔한 답일 수도 있겠지만, 제일 좋은 방법이기도 합니다.
특히 언어논리에 어려움을 겪으신다면, 시중에 나와 있는 ‘논리학’ 관련 도서를 읽는 것도 좋은 방법입니다.
충분한 답변이 되셨는지 모르겠습니다.
감사합니다.
① S의 정보 중 적어도 하나가 참일 확률을 S의 모든 정보가 참일 확률로 나눈 값
갑의 S의 모든 정보가 참일 확률 = 그가 결혼하지 않았으며 비혼일 확률(X+Y+Z)
을의 S의 모든 정보가 참일 확률 = 그가 결혼하지 않았으며 아이가 있을 확률(Q)
여기서 갑은 X+Y+Z이고 을은 Q인지 궁금합니다. 두개의 차이점이 뭔지 모르겠어요.
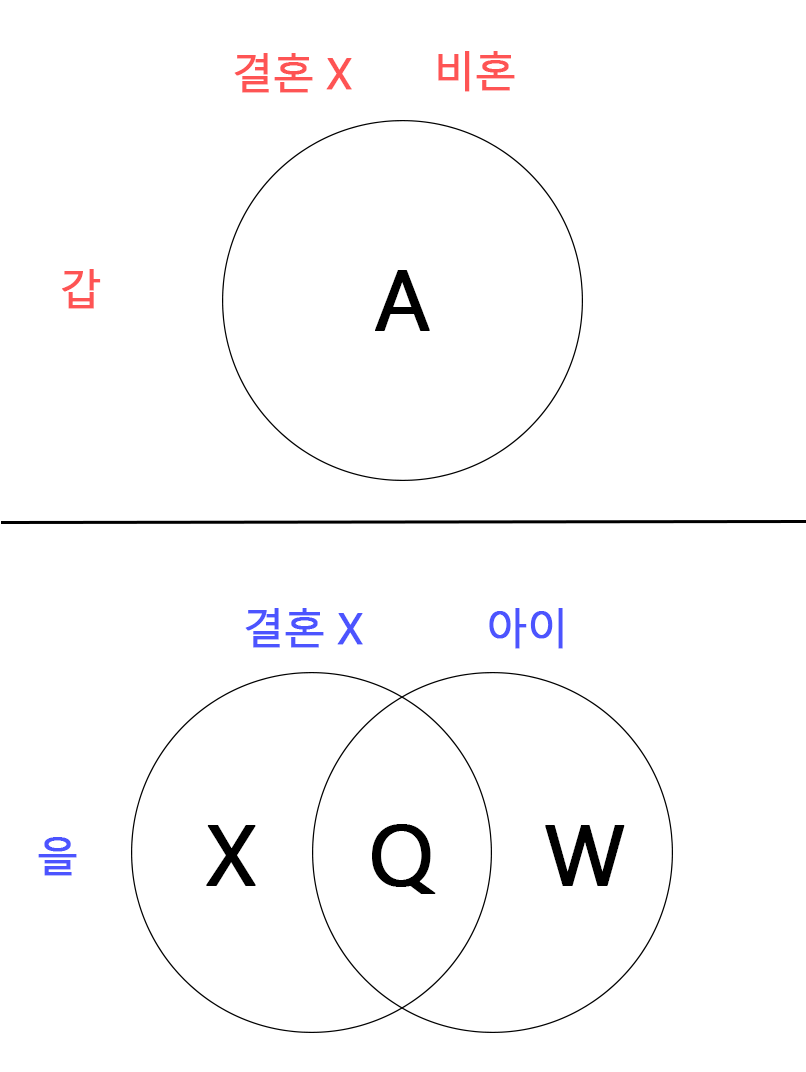
‘그는 결혼하지 않았다.’라는 정보와 ‘그는 비혼이다.’라는 정보는 동일 정보입니다.
이해를 위해 그림에서 ‘결혼 X’ 집합과 ‘비혼’ 집합으로 분리시켰지만 두 집합은 동일 집합입니다.
이 부분에서 혼란을 드린 것 같아 집합 그림을 다시 제작했습니다.
그가 결혼하지 않았으며 비혼일 확률 = A ∧ A = A가 됩니다.
그가 결혼하지 않았으며 아이가 있을 확률은 교집합인 Q가 됩니다.
충분한 설명이 되었는지 모르겠습니다.
궁금한 점이 있으시다면, 언제든지 질문주세요^^