목차
Introduction
There are 15 valid Venn diagrams of categorical syllogisms.
The Logic of Venn Diagrams
Universal Affirmative (A)
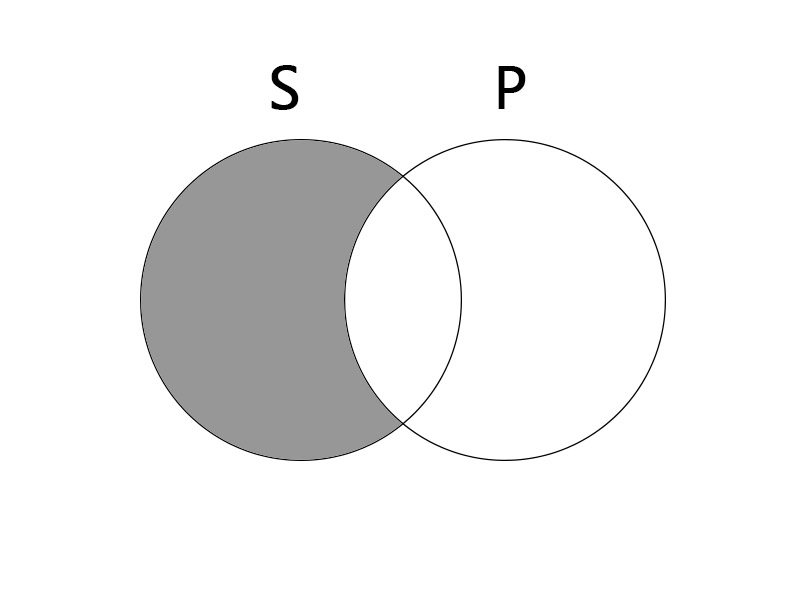 |
All S are P.
Universal Negative (E)
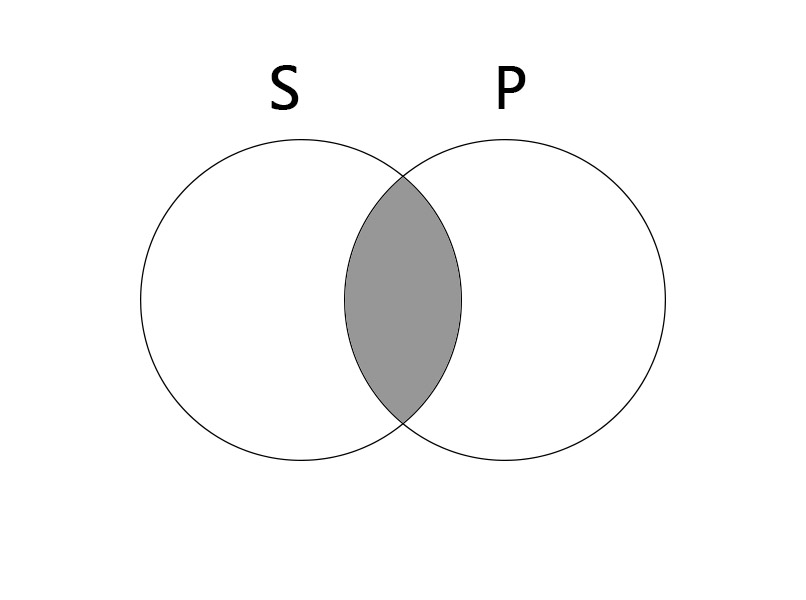 |
No S are P.
Particular Affirmative (I)
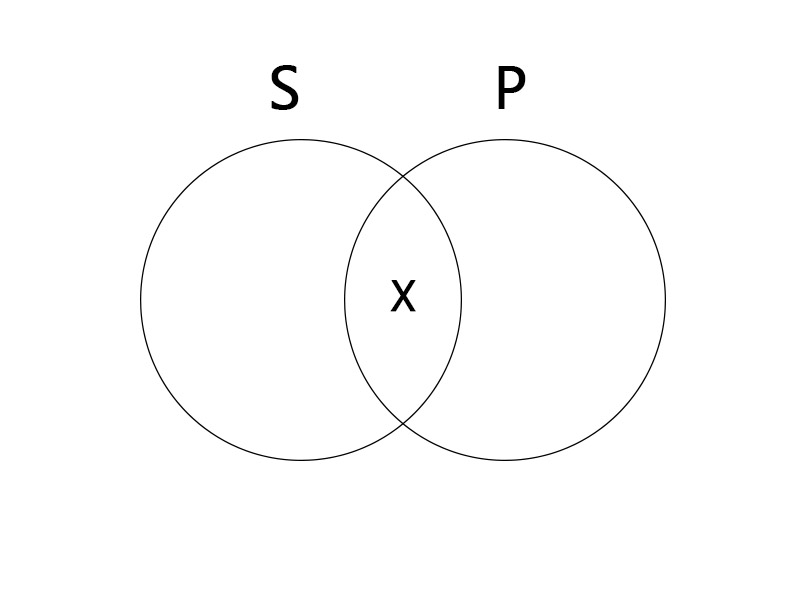 |
Some S are P.
Particular Negative (O)
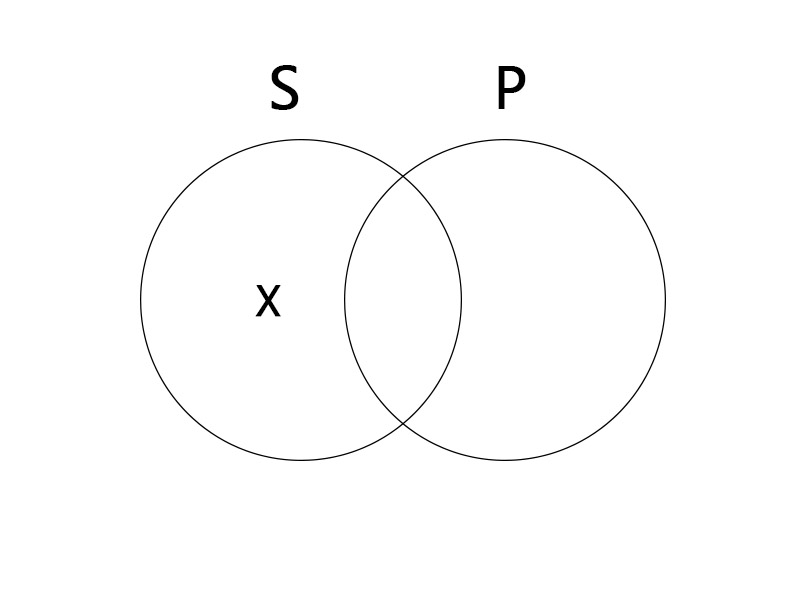 |
Some S are not P.
Categorical Syllogism
The Rules for Valid Categorical Syllogisms
- must have only three terms, each of which designates the same class throughout.
- cannot have two negative premises.
- must have a negative conclusion if either premise is negative.
- cannot have a conclusion with a existential quantity if both premises are universal in quantity.
- must distribute the major term in the major premise if the major term is distributed in the conclusion.
- must have a distributed minor term in the minor premise if the minor term is distributed in the conclusion.
- must have a distributed middle term in at least one premise.
Figures
 |
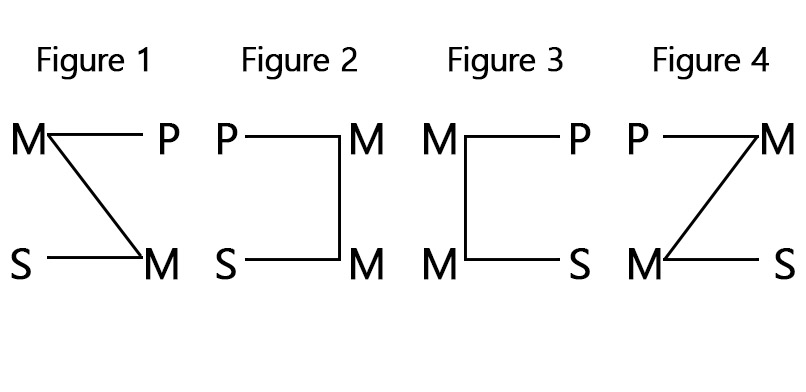 |
Valid Argument Forms
| Figure 1 | AAA, AII, EAE, EIO |
| Figure 2 | AEE, AOO, EAE, EIO |
| Figure 3 | AII, EIO, IAI, OAO |
| Figure 4 | AEE, EIO, IAI |
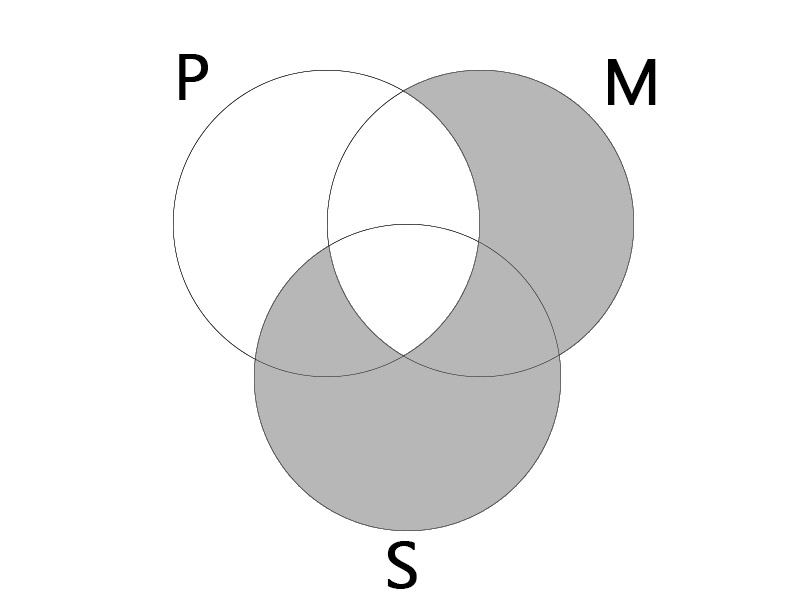
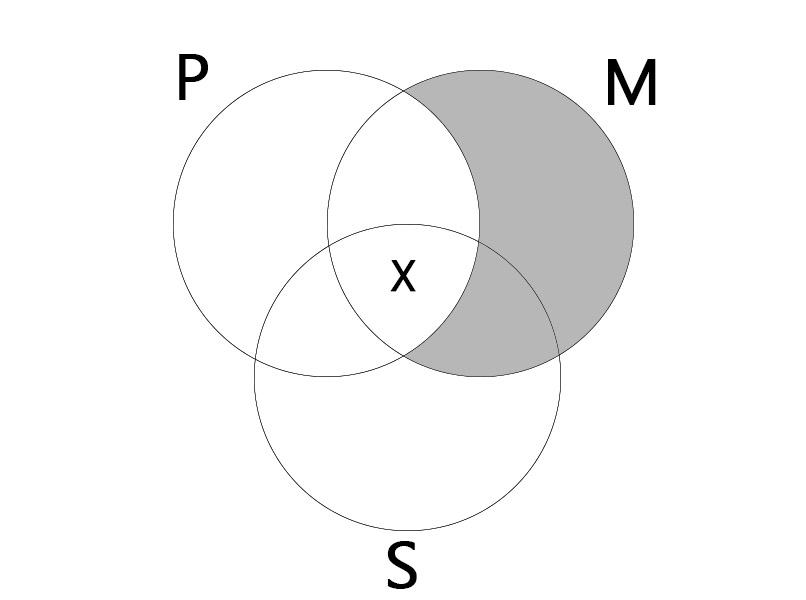
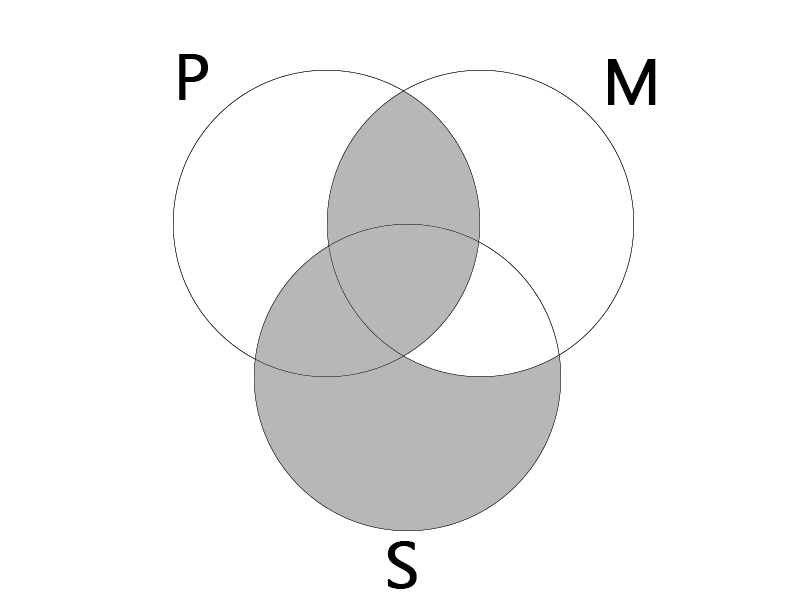
Figure 1
AAA
| All M is P. All S is M. |
| All S is P. |
 |
AII
| All M is P. Some S is M. |
| Some S is P. |
 |
EAE
| No M is P. All S is M. |
| All S is P. |
 |
EIO
| No M is P. Some S is M. |
| Some S is not P. |
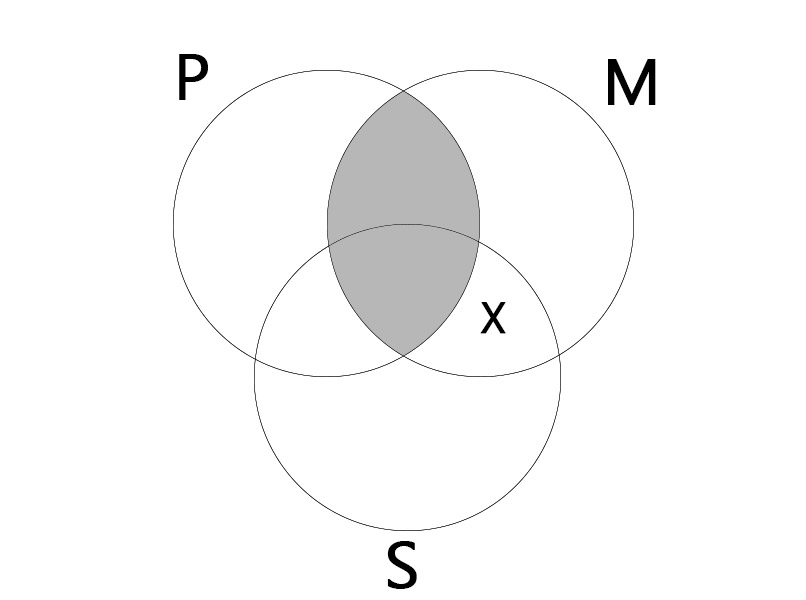 |
Figure 2
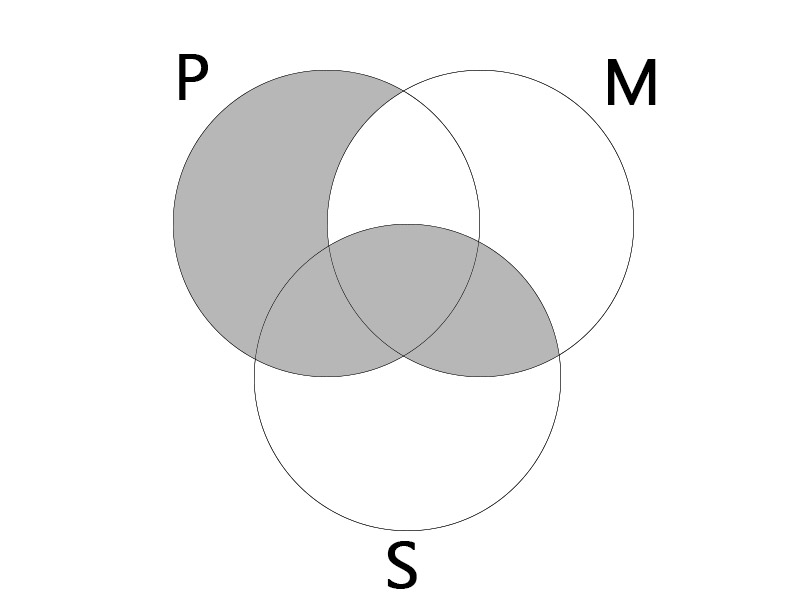
AEE
| All P is M. No S is M. |
| No S is P. |
 |
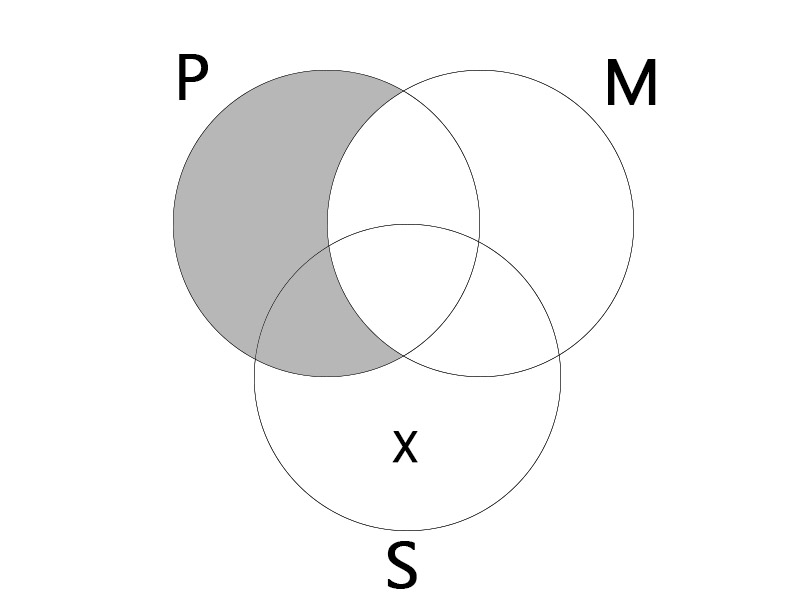
AOO
| All P is M. Some S is not M. |
| Some S is not P. |
 |
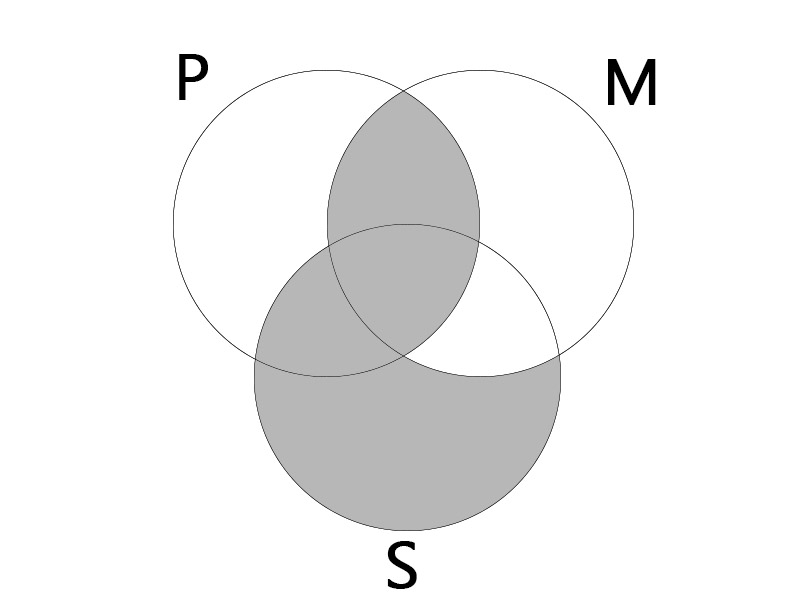
EAE
| No P is M. All S is M. |
| No S is P. |
 |
EIO
| No P is M. Some S is M. |
| Some S is not P. |
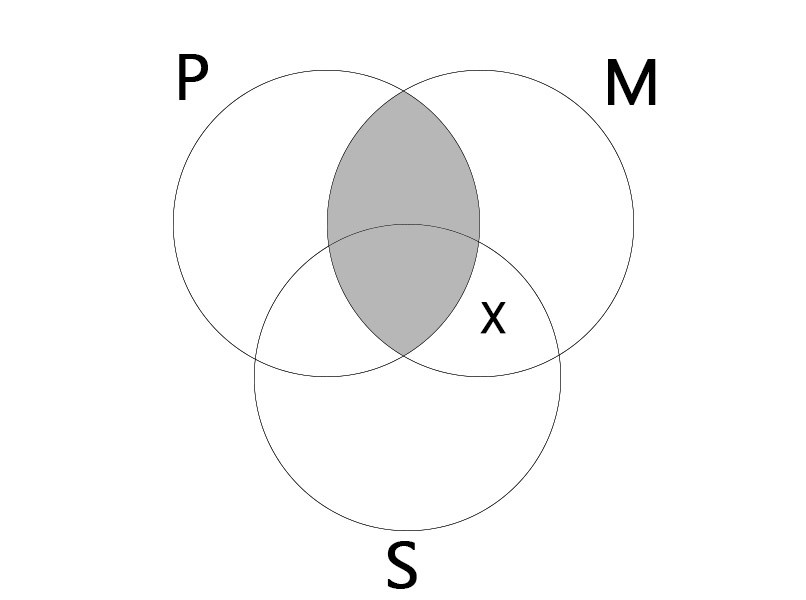 |
Figure 3
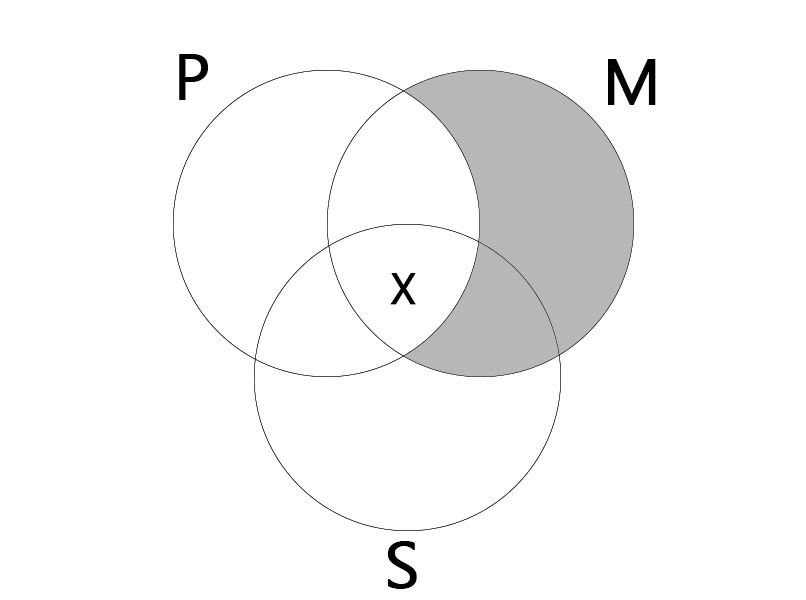
AII
| All M is P. Some M is S. |
| Some S is P. |
 |
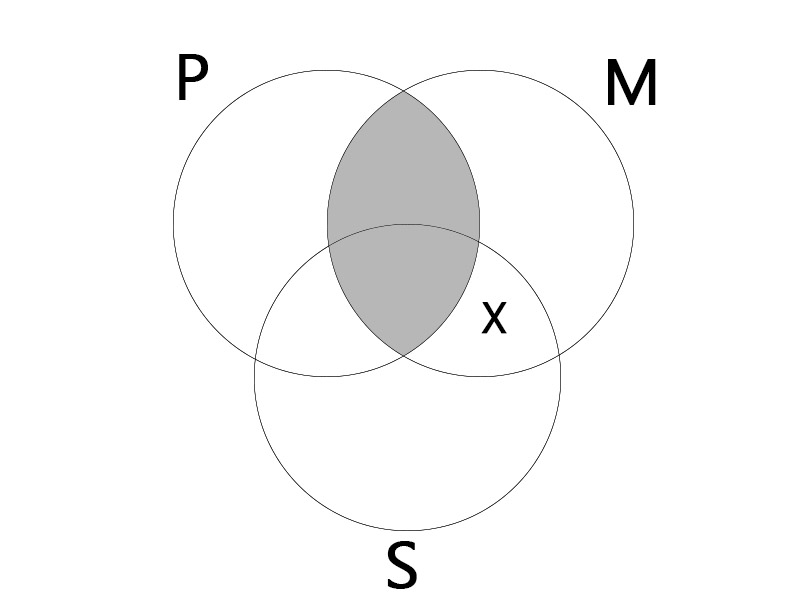
EIO
| No M is P. Some M is S. |
| Some S is not P. |
 |
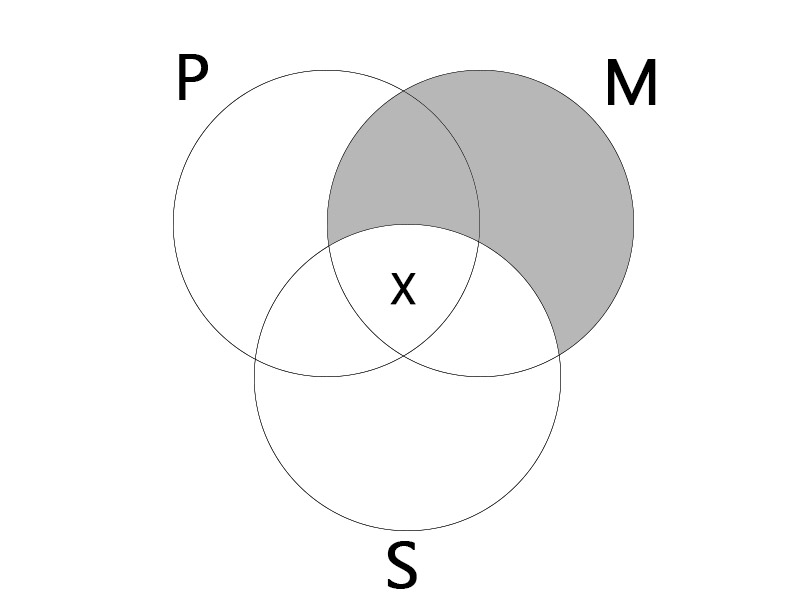
IAI
| Some M is P. All M is S. |
| Some S is P. |
 |
OAO
| Some M is not P. All M is S. |
| Some S is not P. |
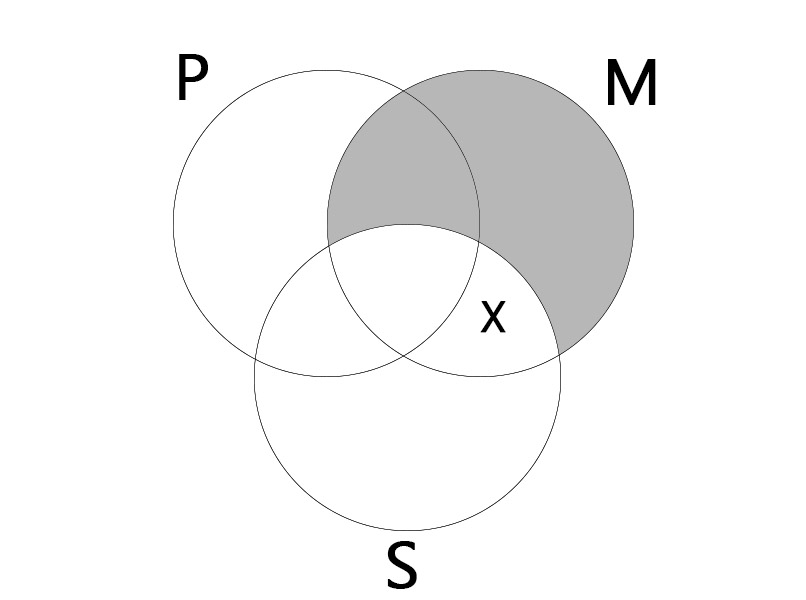 |
Figure 4
AEE
| All P is M. No M is S. |
| No S is P. |
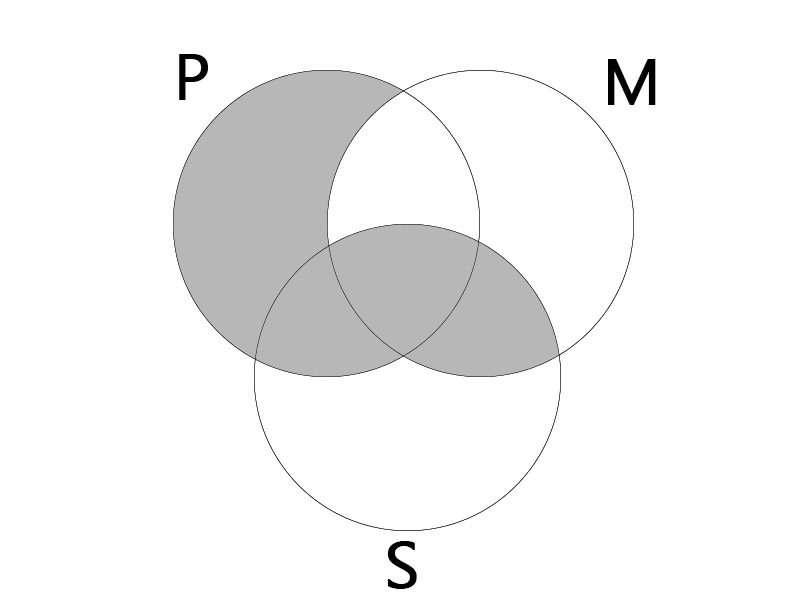 |
EIO
| No P is M. Some M is S. |
| Some S is not P. |
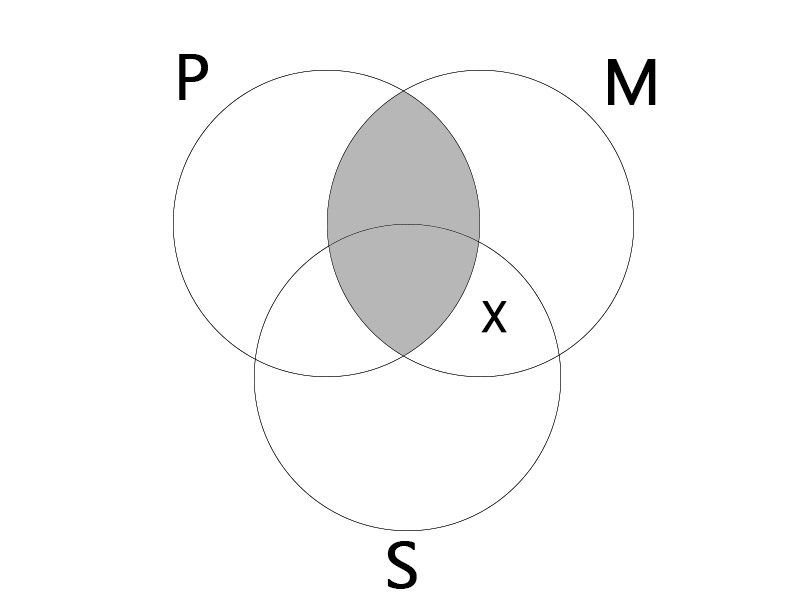 |
IAI
| Some P is M. All M is S. |
| Some S is P. |
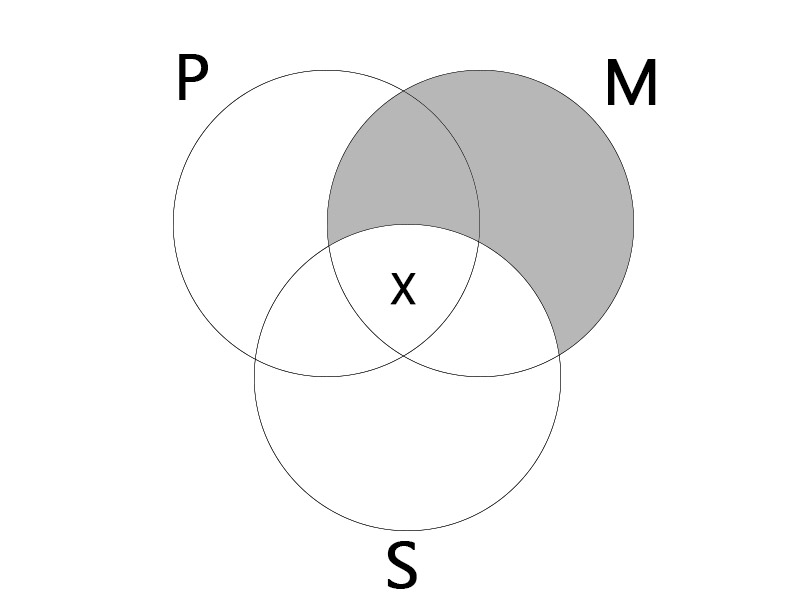 |

