[9급 국어] 9급 공무원 국어 출제기조 전환 예시문제 20번 해설 – 문학 자연 예술 정언명제 삼단논법 벤다이어그램

1 개요
2 문제
3 문제 해설
4 9급 국어 출제기조 전환 예시문제
5 정언논리 기출문제
6 9급 국가직 공무원 국어 시험
7 9급 국가직 공무원 시험
8 9급 공무원 시험
9 PSAT 논리 구조 문제
10 공무원 PSAT 기출

개요

다음은 9급 국어 출제기조 전환 예시문제 20번 문제 해설이다.

문제

20. 다음 글의 밑줄 친 결론을 이끌어내기 위해 추가해야 할 것은?

문학을 좋아하는 사람은 모두 자연의 아름다움을 좋아하는 사람이다. 자연의 아름다움을 좋아하는 어떤 사람은 예술을 좋아하는 사람이다. 따라서 예술을 좋아하는 어떤 사람은 문학을 좋아하는 사람이다.

① 자연의 아름다움을 좋아하는 사람은 모두 문학을 좋아하는 사람이다.

② 문학을 좋아하는 어떤 사람은 자연의 아름다움을 좋아하는 사람이다.

③ 예술을 좋아하는 어떤 사람은 자연의 아름다움을 좋아하는 사람이다.

④ 예술을 좋아하지만 문학을 좋아하지 않는 사람은 모두 자연의 아름다움을 좋아하는 사람이다.

출처: 사이버국가고시센터

문제 해설

정언논리 삼단논법의 벤다이어그램 풀이 방법이다.

문학을 좋아하는 사람 = 문학

자연의 아름다움을 좋아하는 사람 = 자연

예술을 좋아하는 사람 = 예술

문학을 좋아하는 사람은 모두 자연의 아름다움을 좋아하는 사람이다.

위 명제를 벤다이어그램으로 나타내면 위와 같다. 회색 영역은 비어있다는 뜻이다.

자연의 아름다움을 좋아하는 어떤 사람은 예술을 좋아하는 사람이다.

자연의 아름다움을 좋아하는 모두가 사람은 예술을 좋아하는 사람이 아니라 일부 ‘어떤’ 사람이기 때문에 빨간색 X로 해당 영역을 표시했다.

예술을 좋아하는 어떤 사람은 문학을 좋아하는 사람이다.

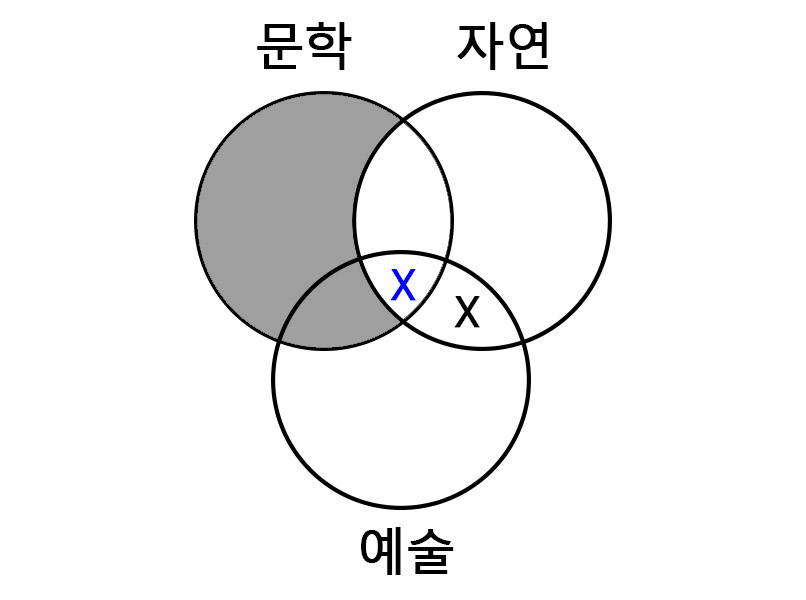예술을 좋아하는 어떤 사람은 문학을 좋아하는 사람이기 때문에 최종적으로 파란색 X가 있는 영역이 결론이 된다.

그렇다면 검은색 X 영역이 지워지는 전제가 추가되어야 결론이 도출된다.

① 자연의 아름다움을 좋아하는 사람은 모두 문학을 좋아하는 사람이다.

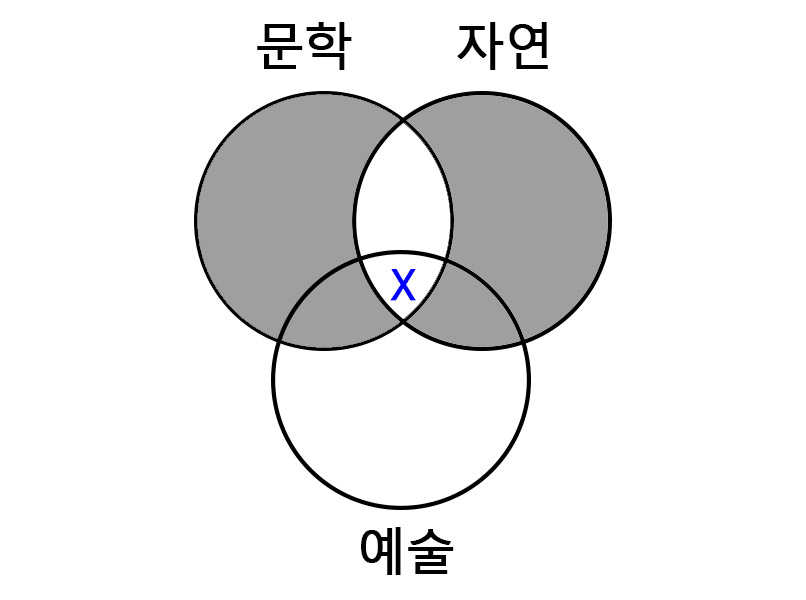전제에서 ‘문학을 좋아하는 사람은 모두 자연의 아름다움을 좋아하는 사람이다’라고 했다.

보기의 내용이 사실이라면 결국 문학을 좋아하는 사람과 자연의 아름다움을 좋아하는 사람은 모두 같다. 위와 같이 문학과 자연의 교집합으로 표현할 수 있다.

그렇다면 검은색 X 영역이 지워지고 파란색 X 영역만 남는다.

그리고 결론 ‘예술을 좋아하는 어떤 사람은 문학을 좋아하는 사람이다’가 도출된다.

따라서 보기의 내용은 옳다.

② 문학을 좋아하는 어떤 사람은 자연의 아름다움을 좋아하는 사람이다.

이미 전제에서 ‘문학을 좋아하는 사람은 모두 자연의 아름다움을 좋아하는 사람이다’가 전제로 제시되었기 때문에 보기의 내용은 결론을 도출하기 위한 전제가 될 수 없다. 검은색 X 영역이 지워지지 않기 때문이다.

빨간색 X는 ‘문학을 좋아하는 어떤 사람은 자연의 아름다움을 좋아하는 사람이다’에 해당하는 것을 표시한 것이다. 경계선 위에 표시한 이유는 빨간색 X가 해당하는 영역이 A영역 또는 B영역 또는 A와 B영역에 해당할 수 있다는 것을 나타내기 위해서다.

참고로 정언명제에서 ‘문학을 좋아하는 사람은 모두 자연의 아름다움을 좋아하는 사람이다’는 ‘문학을 좋아하는 어떤 사람은 자연의 아름다움을 좋아하는 사람이다’를 ‘논리적으로 함축한다’라고 표현한다.

따라서 보기의 내용은 옳지 않다.

③ 예술을 좋아하는 어떤 사람은 자연의 아름다움을 좋아하는 사람이다.

보기의 내용을 벤다이어그램으로 나타내면 위와 같다.

빨간색 X에 해당하는 영역은 A영역 또는 B영역 또는 A와 B영역이다.

결론은 A영역이 아닌 B영역인데, 보기의 내용에 따르면 A영역이 지워지지 않는다.

따라서 보기의 내용은 옳지 않다.

④ 예술을 좋아하지만 문학을 좋아하지 않는 사람은 모두 자연의 아름다움을 좋아하는 사람이다.

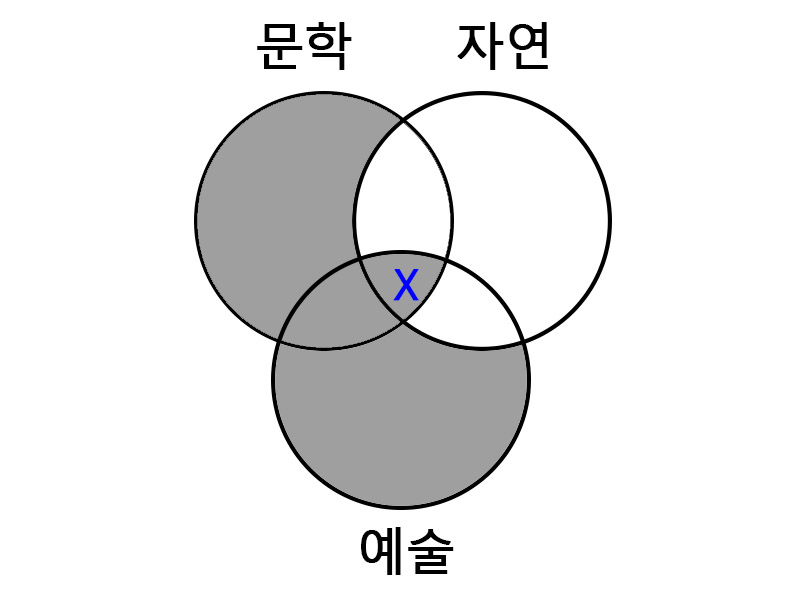보기의 내용에 따르면 결론 부분이 지워진다.

따라서 보기의 내용은 옳지 않다.

더 자세한 내용은 정언명제 삼단논법 참조.

정답은 ①번이다.

개요

문제

문제 해설

9급 국어 출제기조 전환 예시문제

정언논리 기출문제

9급 국가직 공무원 국어 시험

9급 국가직 공무원 시험

9급 공무원 시험

PSAT 논리 구조 문제

공무원 PSAT 기출

답글 남기기 응답 취소