개요
다음은 2011년 국가공무원 5급 언어논리영역 우책형 14번 문제 해설이다.
문제
문 14. 다음 글로부터 올바른 추론을 하고 있는 사람을 <보기>에서 모두 고르면?
| 아리스토텔레스가 얼마나 위대한지는 삼단논법의 타당성을 증명한 그의 방식만 보아도 알 수 있다. 가령 다음과 같은 삼단논법을 생각해보자.
(가) 여학생은 모두 화장을 한다. (나) 우리반 학생 가운데 일부는 화장을 하지 않는다. 따라서 (다) 우리반 학생 가운데 일부는 여학생이 아니다. 그는 이 삼단논법의 전제가 모두 참이라면 결론도 참일 수밖에 없음을 다음과 같이 증명한다. 우선 논의를 위해 이 논증의 전제는 모두 참인데 결론은 거짓이라고 가정해보자. 결론 (다)가 거짓이라면, (다)와 모순인 (바) 화장을 하는 학생 가운데 일부는 여학생이 아니다. (사) 화장을 하는 학생은 모두 우리반 학생이다. 따라서 (아) 우리반 학생 가운데 일부는 여학생이 아니다. 앞서처럼 이 논증의 전제는 모두 참인데 결론은 거짓이라고 가정해보자. 결론 (아)가 거짓이라면, (아)와 모순인 |
| <보 기> |
| 지훈: (라)와 (자)에는 같은 명제가 들어가는군.
연길: (마)와 (차)에 들어갈 각 명제가 참이라면 (라)에 들어갈 명제도 참일 수밖에 없겠군. 혁진: (라)와 (마)에 들어갈 각 명제가 참이라면 (차)에 들어갈 명제도 참일 수밖에 없겠군. |
① 연길
② 혁진
③ 지훈, 연길
④ 지훈, 혁진
⑤ 지훈, 연길, 혁진
출처: 사이버국가고시센터
문제 해설
이 문제는 정언 논리에 대한 내용이다.
결론 (다)가 거짓이라면, (다)와 모순인 (라) 가 참임을 추리해 낼 수 있다.
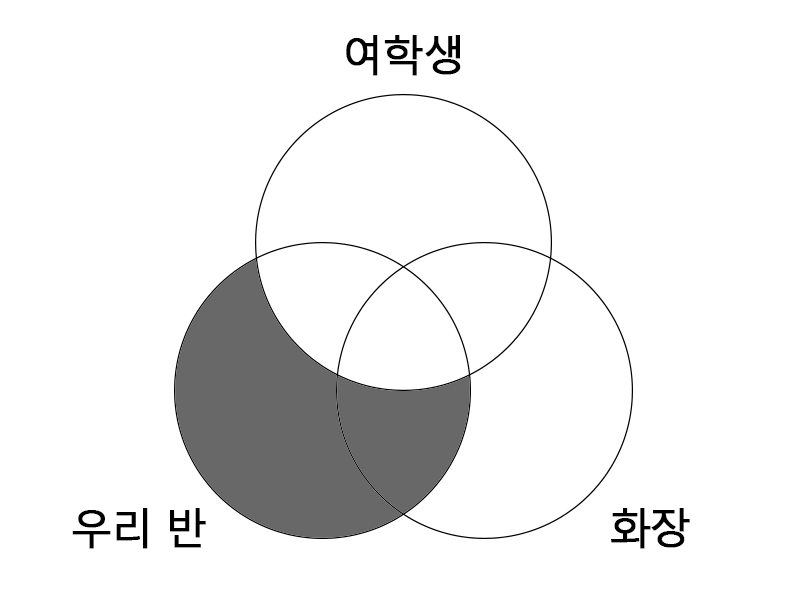
(다) 우리반 학생 가운데 일부는 여학생이 아니다. |
(라) 우리반 학생 모두 여학생이다.
(다)와 모순인 명제는 ‘우리반 학생 모두 여학생이다’이다.
(라)와 (가)로부터 우리는 (마) 가 참이라는 것도 알아낼 수 있다.
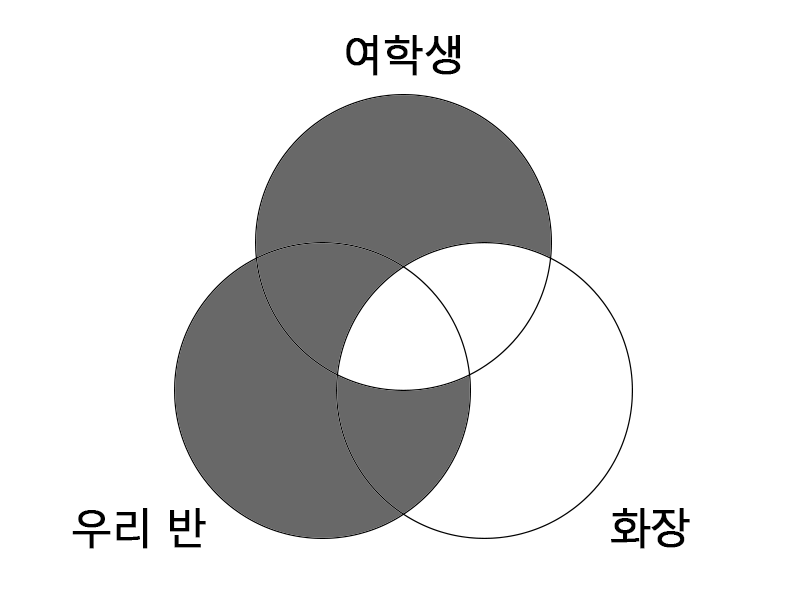
(라) 우리반 학생 모두 여학생이다.
(가) 여학생은 모두 화장을 한다.
|
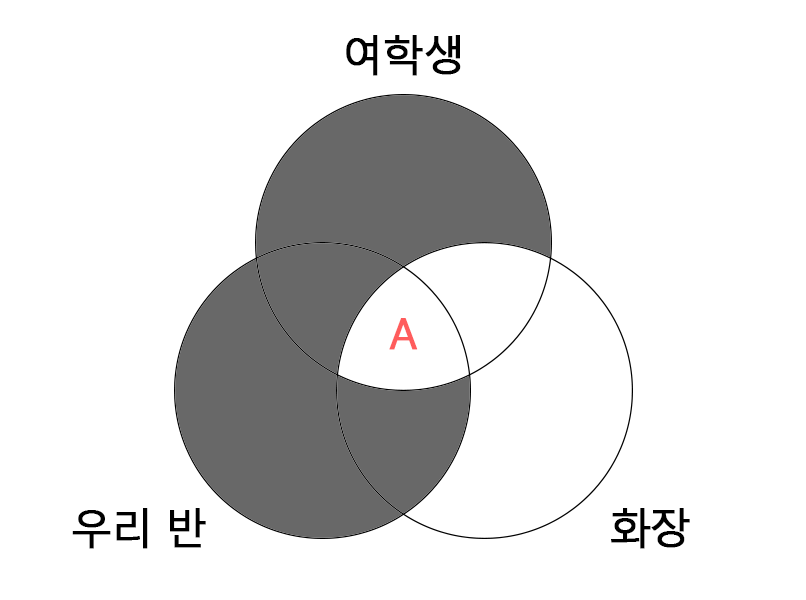 |
(마) 우리 반 학생 모두(A) 화장을 한다.
결론 (아)가 거짓이라면, (아)와 모순인 (자) 가 참임을 알 수 있다.
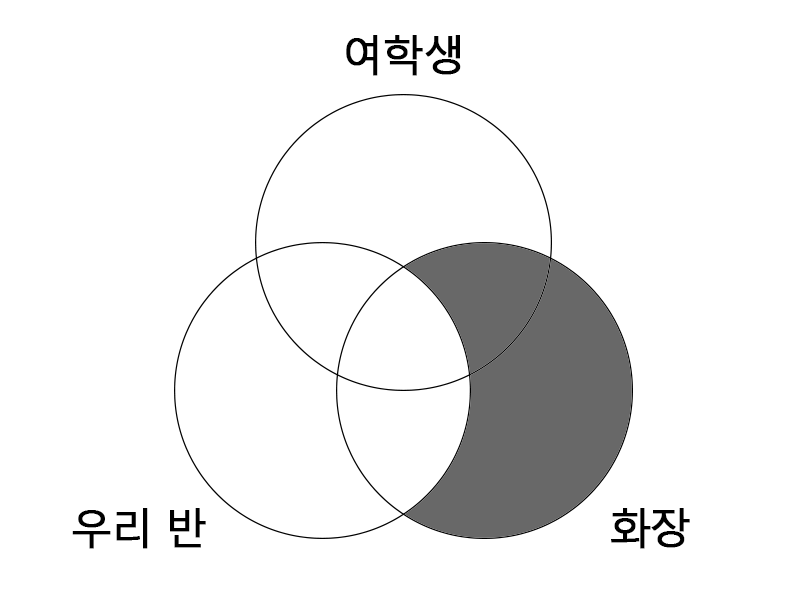
(아) 우리반 학생 가운데 일부는 여학생이 아니다. |
(자) 우리반 학생 모두 여학생이다.
(아)와 모순인 명제는 ‘우리반 학생 모두 여학생이다’이다.
(사)와 (자)가 참이라는 것으로부터 (차) 가 참이라는 사실도 알아낼 수 있다.
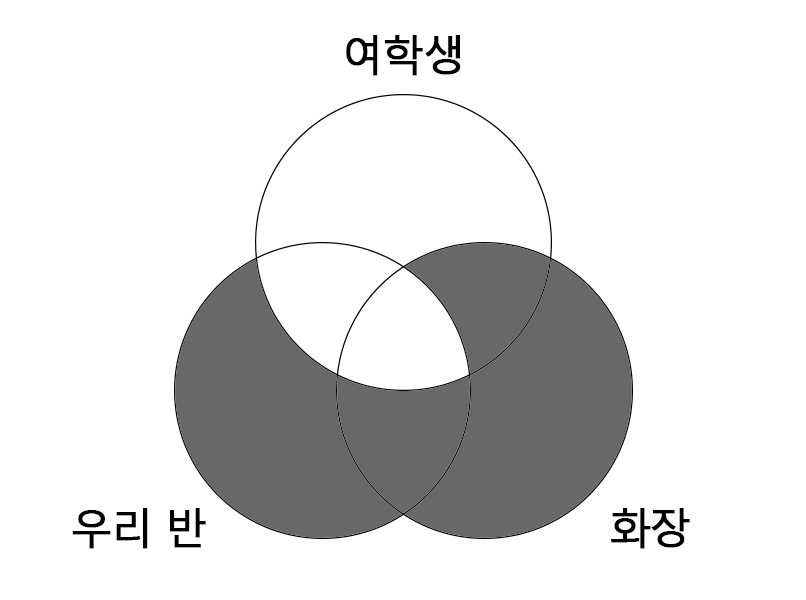
(사) 화장을 하는 학생은 모두 우리반 학생이다.
(자) 우리반 학생 모두 여학생이다.
|
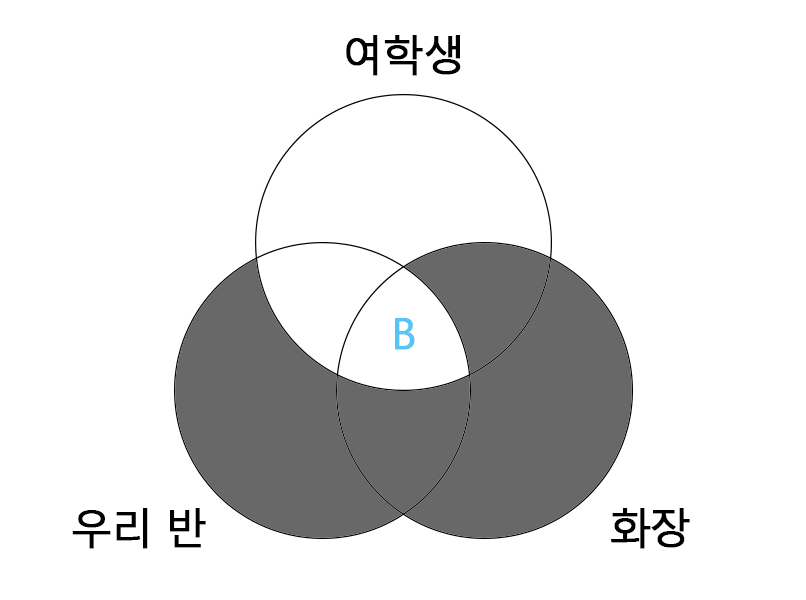 |
(차) 화장을 하는 학생 모두(B) 여학생이다.
지훈: (라)와 (자)에는 같은 명제가 들어가는군.
| (라) 우리반 학생 모두 여학생이다.
(자) 우리반 학생 모두 여학생이다. |
따라서 보기의 내용은 옳다.
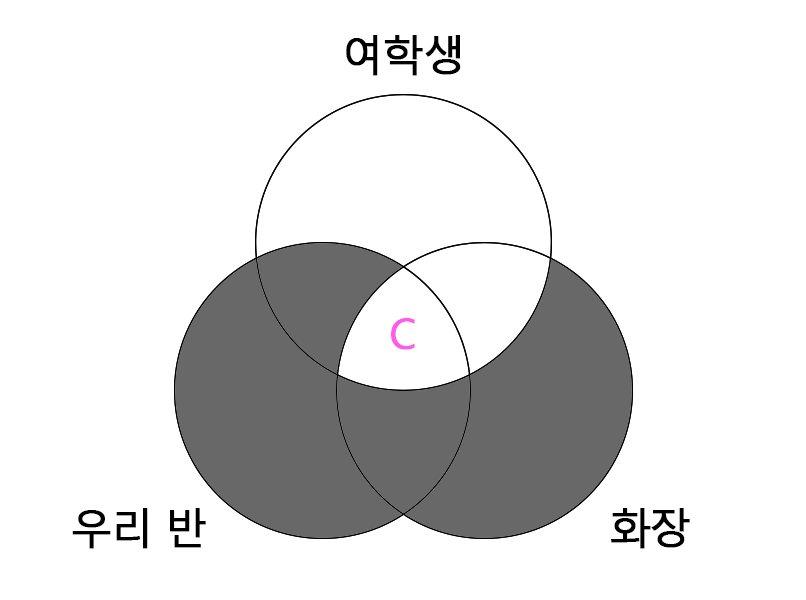
연길: (마)와 (차)에 들어갈 각 명제가 참이라면 (라)에 들어갈 명제도 참일 수밖에 없겠군.
(마) 우리 반 학생 모두 화장을 한다.
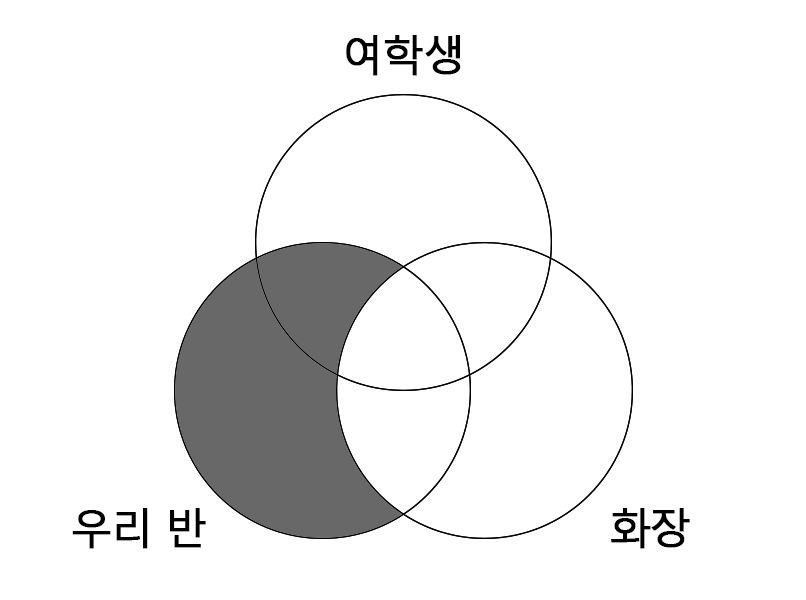 |
(차) 화장을 하는 학생 모두 여학생이다.
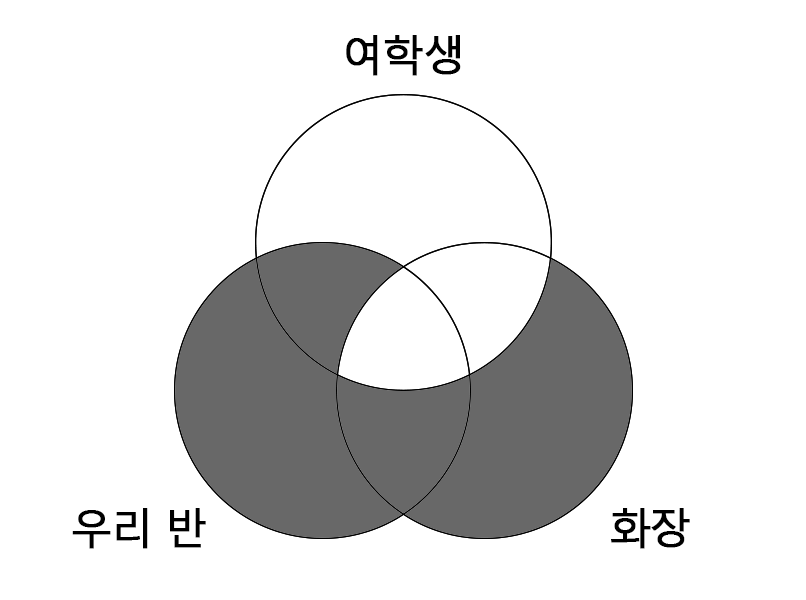 |
(라) 우리반 학생 모두(C) 여학생이다.
 |
따라서 보기의 내용은 옳다.
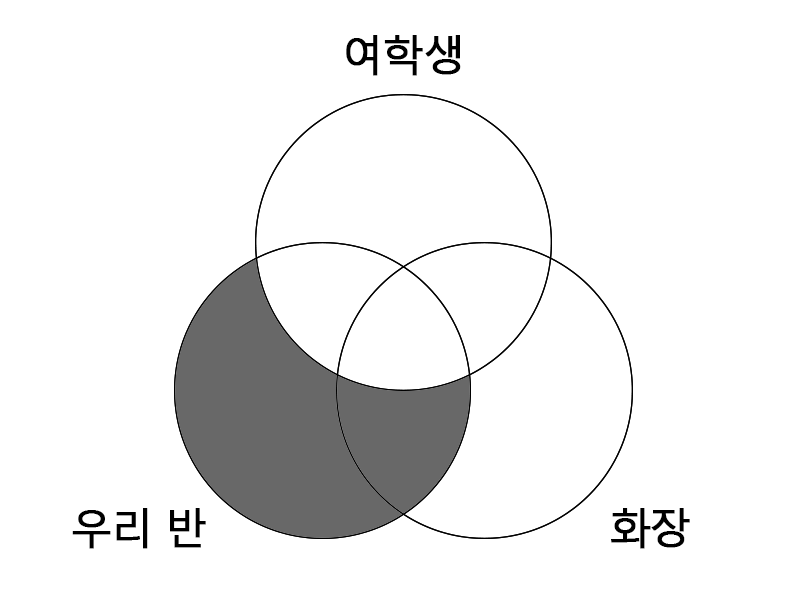
혁진: (라)와 (마)에 들어갈 각 명제가 참이라면 (차)에 들어갈 명제도 참일 수밖에 없겠군.
(라) 우리반 학생 모두 여학생이다.
 |
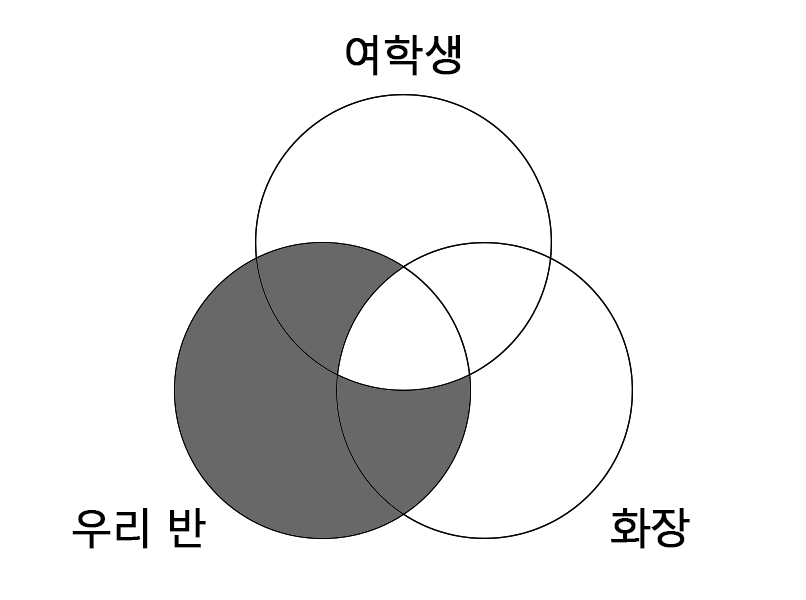
(마) 우리반 학생 모두 화장을 한다.
 |
(차) 화장을 하는 학생 모두 여학생이다.
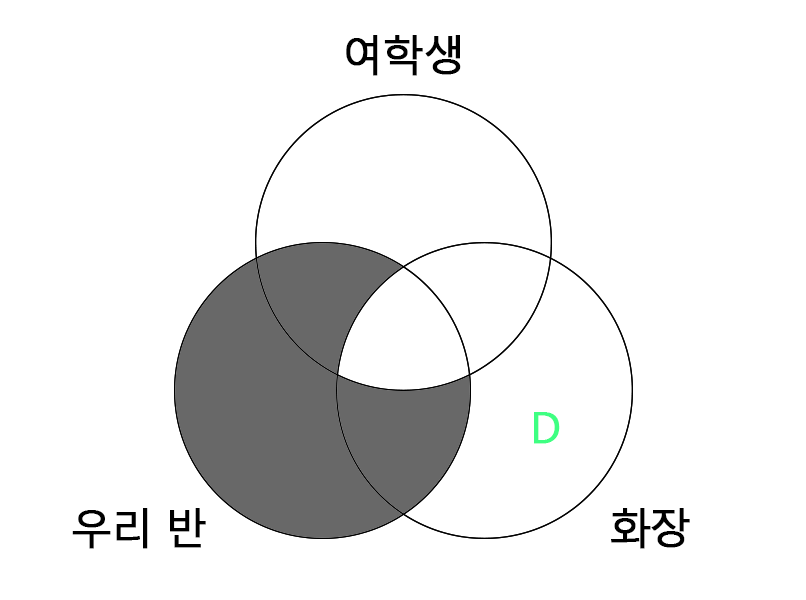 |
화장을 하는 학생 중에는 남학생(D)도 있을 수 있다. 그러므로 화장을 하는 학생 모두 여학생이 될 수 없다.
따라서 보기의 내용은 옳지 않다.
정답은 ③번이다.
2011 5급 PSAT 언어논리
- [PSAT 기출] 2011 5급 언어논리 우책형 39번 40번 해설 – 유행성 독감 예방접종
- [PSAT 기출] 2011 5급 언어논리 우책형 38번 해설 – 임신 태아 치료 추론
- [PSAT 기출] 2011 5급 언어논리 우책형 37번 해설 – 공직자 윤리 명제 논리
- [PSAT 기출] 2011 5급 언어논리 우책형 36번 해설 – 의사소통 정보해석능력 명제 논리
- [PSAT 기출] 2011 5급 언어논리 우책형 35번 해설 – 반박 논쟁 차원
- [PSAT 기출] 2011 5급 언어논리 우책형 34번 해설 – 개화식물 단일식물 광주기 개화 추론
- [PSAT 기출] 2011 5급 언어논리 우책형 33번 해설 – 고생물 화석 추론
- [PSAT 기출] 2011 5급 언어논리 우책형 32번 해설 – 달리기 시합 논리퀴즈
- [PSAT 기출] 2011 5급 언어논리 우책형 31번 해설 – 탈레스 베이컨 아낙시만드로스
- [PSAT 기출] 2011 5급 언어논리 우책형 30번 해설 – 배분원칙
- [PSAT 기출] 2011 5급 언어논리 우책형 29번 해설 – 슈미트 쿠르트
- [PSAT 기출] 2011 5급 언어논리 우책형 28번 해설 – 생존 윤리원칙 장기이식
- [PSAT 기출] 2011 5급 언어논리 우책형 27번 해설 – 벤젠 노출 농도 직업안전보건국
- [PSAT 기출] 2011 5급 언어논리 우책형 26번 해설 – 고구려 벽화고문 생활풍속도 사신도
- [PSAT 기출] 2011 5급 언어논리 우책형 25번 해설 – 박지원 교우론
- [PSAT 기출] 2011 5급 언어논리 우책형 24번 해설 – 이슬람 중동 아랍
- [PSAT 기출] 2011 5급 언어논리 우책형 23번 해설 – 영국 지리학자 기행문 연해주 이주
- [PSAT 기출] 2011 5급 언어논리 우책형 22번 해설 – 인문학
- [PSAT 기출] 2011 5급 언어논리 우책형 21번 해설 – 붕당 과거제도
- [PSAT 기출] 2011 5급 언어논리 우책형 19번 20번 해설 – 까마귀 역설 명제 논리 추론
- [PSAT 기출] 2011 5급 언어논리 우책형 18번 해설 – 범인 머리카락 갈색 명제논리 논리퀴즈
- [PSAT 기출] 2011 5급 언어논리 우책형 17번 해설 – 기술 과학 논지 강화
- [PSAT 기출] 2011 5급 언어논리 우책형 16번 해설 – 여섯 개 묘듈 명제논리 논리퀴즈
- [PSAT 기출] 2011 5급 언어논리 우책형 15번 해설 – 믿음 A 미술관 위치정보
- [PSAT 기출] 2011 5급 언어논리 우책형 14번 해설 – 아리스토텔레스 삼단논법 정언 논리
- [PSAT 기출] 2011 5급 언어논리 우책형 13번 해설 – 실현니치 기본니치
- [PSAT 기출] 2011 5급 언어논리 우책형 12번 해설 – 빨간색 꽃 분홍색 가설
- [PSAT 기출] 2011 5급 언어논리 우책형 11번 해설 – 원격진료
- [PSAT 기출] 2011 5급 언어논리 우책형 10번 해설 – 윤리적 용어 양립
- [PSAT 기출] 2011 5급 언어논리 우책형 9번 해설 – 부사적 지능 명사적 지능
- [PSAT 기출] 2011 5급 언어논리 우책형 8번 해설 – 화이사상 나래주의 중체서용
- [PSAT 기출] 2011 5급 언어논리 우책형 7번 해설 – 모두스 비벤디
- [PSAT 기출] 2011 5급 언어논리 우책형 6번 해설 – 원자핵 양성자 동위원소
- [PSAT 기출] 2011 5급 언어논리 우책형 5번 해설 – 설헌 금운 국란
- [PSAT 기출] 2011 5급 언어논리 우책형 4번 해설 – 부패 반부패 개도국
- [PSAT 기출] 2011 5급 언어논리 우책형 3번 해설 – 파시즘 고전적 독재
- [PSAT 기출] 2011 5급 언어논리 우책형 2번 해설 – 수학 자연 해석 묘사
- [PSAT 기출] 2011 5급 언어논리 우책형 1번 해설 – 언문
관련 문서
- 2011 5급 PSAT 해설 모음
- 5급 PSAT 언어논리 해설 모음
- 5급 PSAT 해설 모음
- 국가직 7급 PSAT 언어논리 해설 모음
- 국가직 7급 PSAT 해설 모음
- 민경채 PSAT 언어논리 해설 모음
- 민경채 PSAT 해설 모음
- PSAT 기출 해설 모음
- PSAT 명제 논리 문제 해설 모음
- PSAT 정언 논리 문제 해설 모음
- 정언 논리 공부 자료
- PSAT 추론 문제 해설 모음
- PSAT 강화 약화 문제 해설 모음
- PSAT 법조문 문제 해설 모음
- PSAT 논리퀴즈 문제 해설 모음