[PSAT 기출] 2020 민경채 상황판단 가책형 21번 해설 – 키 어린이 뒤통수 논리퀴즈

1 개요
2 문제
3 문제 해설
4 2020 민경채 PSAT 상황판단
5 관련 문서

개요

다음은 2020년 국가공무원 민간경력자(민경채) 상황판단영역 가책형 21번 문제다.

문제

문 21. 다음 글을 근거로 판단할 때, <보기>에서 옳은 것만을 모두 고르면?

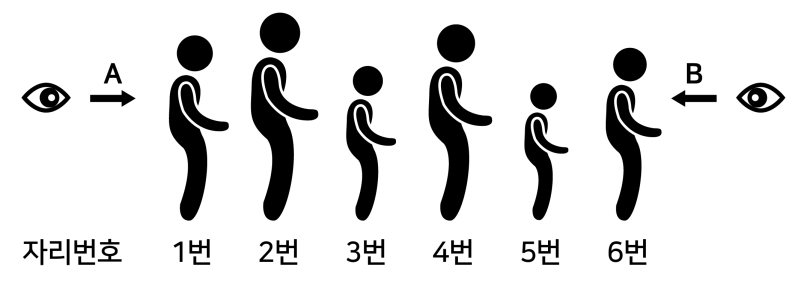
키가 서로 다른 6명의 어린이를 다음 그림과 같이 한 방향을 바라보도록 일렬로 세우려고 한다. 그림은 일렬로 세운 하나의 예이다. 한 어린이(이하 甲이라 한다)의 등 뒤에 甲보다 키가 큰 어린이가 1명이라도 있으면 A방향에서 甲의 뒤통수는 보이지 않고, 1명도 없으면 A방향에서 甲의 뒤통수는 보인다. 반대로 甲의 앞에 甲보다 키가 큰 어린이가 1명이라도 있으면 B방향에서 甲의 얼굴은 보이지 않고, 1명도 없으면 B방향에서 甲의 얼굴은 보인다.

<보 기>

ㄱ. A방향에서 보았을 때 모든 어린이의 뒤통수가 다 보이게 세우는 방법은 1가지뿐이다.

ㄴ. 키가 세 번째로 큰 어린이를 5번 자리에 세운다면, A방향에서 보았을 때 그 어린이의 뒤통수는 보이지 않는다.

ㄷ. B방향에서 2명의 얼굴만 보이도록 어린이들을 세웠을 때, A방향에서 6번 자리에 서 있는 어린이의 뒤통수는 보이지 않는다.

ㄹ. B방향에서 3명의 얼굴이 보인다면, A방향에서 4명의 뒤통수가 보일 수 없다.

① ㄱ, ㄴ

② ㄷ, ㄹ

③ ㄱ, ㄴ, ㄷ

④ ㄱ, ㄷ, ㄹ

⑤ ㄴ, ㄷ, ㄹ

출처: 사이버국가고시센터

문제 해설

키가 제일 작은 어린이부터 제일 큰 어린이까지 순서대로 1부터 6까지의 숫자를 부여한다.

ㄱ. A방향에서 보았을 때 모든 어린이의 뒤통수가 다 보이게 세우는 방법은 1가지뿐이다.

A방향에서 B방향까지 숫자 1, 2, 3, 4, 5, 6를 순서대로 놓는다. 그렇게 하면 A방향에서 보았을 때 모든 숫자가 순차대로 커지는 것을 볼 수 있다. 이것 이외에는 모든 어린이의 뒤통수가 다 보이게 할 수 있는 줄 세우기는 없다.

1 – 2 – 3 – 4 – 5 – 6

만약 중간에 숫자 순서가 하나라도 바뀐다면 한 숫자보다 더 큰 다른 숫자가 A방향에 가깝게 위치하여 모든 어린이의 뒤통수가 다 보이지 않는다.

따라서 보기의 내용은 옳다.

ㄴ. 키가 세 번째로 큰 어린이를 5번 자리에 세운다면, A방향에서 보았을 때 그 어린이의 뒤통수는 보이지 않는다.

키가 세 번째로 큰 어린이는 숫자 4다. 5번 자리에 숫자 4를 놓고, 6번 자리에 숫자 5 또는 6을 놓는다. 그렇다면 5번 자리 왼쪽으로 숫자 6번 자리에 놓이지 않은 숫자 5 또는 6이 온다.

1 – 2 – 3 – 6 – 4 – 5

5번 자리 왼쪽으로 숫자 4보다 더 큰 숫자가 오는 것은 키가 세 번째로 큰 어린이의 뒤통수가 보이지 않게 되는 것과 같다.

따라서 보기의 내용은 옳다.

ㄷ. B방향에서 2명의 얼굴만 보이도록 어린이들을 세웠을 때, A방향에서 6번 자리에 서 있는 어린이의 뒤통수는 보이지 않는다.

B방향에서 2명의 얼굴만 보이도록 어린이들을 세우는 방법은 5번 자리에 숫자 6, 6번 자리에 나머지 숫자 중 하나를 놓는다. 그렇게 되면 A방향에서 6번 자리에 서 있는 어린이의 뒤통수는 보이지 않는다.

2 – 3 – 4 – 5 – 6 – 1

따라서 보기의 내용은 옳다.

ㄹ. B방향에서 3명의 얼굴이 보인다면, A방향에서 4명의 뒤통수가 보일 수 없다.

B방향에서 3명의 얼굴이 보이게 하려면, 4번 자리에 숫자 6, 5번 자리에 숫자 5, 6번 자리에 숫자 4를 놓으면 된다.

이 상태에서 1번 자리에 숫자 1, 2번 자리에 숫자 2, 3번 자리에 숫자 3, 4번 자리에 숫자 6이 놓인다면 A방향에서 4명의 뒤통수가 보일 수 있다.

1 – 2 – 3 – 6 – 5 – 4

따라서 보기의 내용은 옳지 않다.

정답은 ③번이다.

개요

문제

문제 해설

2020 민경채 PSAT 상황판단

관련 문서

답글 남기기 응답 취소