[정언논리] 정언명제 정언삼단논법 정리 (벤 다이어그램 PSAT LEET)

글쓴이 조나탕작성일자 카테고리 공부자료태그 , , , , ,

개요

다음은 정언 논리, 정언명제, 삼단논법, 벤 다이어그램 등을 정리한 것이다.

정언명제 종류

정언명제 양 질 명칭 유형
모든 S는 P이다.
All S are P.		 전칭 긍정 전칭긍정명제
Universal affirmative		 A
어떤 S도 P가 아니다.
No S are P.		 전칭 부정 전칭부정명제
Universal negative		 E
어떤 S는 P이다.
Some S are P.		 특칭 긍정 특칭긍정명제
Particular affirmative		 I
어떤 S는 P가 아니다.
Some S are not P.		 측징 부정 특칭부정명제
Particular negative		 O

 

전칭긍정명제(Universal affirmative)

모든 S는 P이다. All S are P.

예) 모든 남성은 인간이다. 모든 개는 동물이다.

전칭긍정명제는 대문자 A로 표현하기도 한다.

 

전칭부정명제(Universal negative)

어떤 S도 P가 아니다. No S are P.

예) 어떤 서울 시민도 외계인이 아니다. 어떤 고양이도 개가 아니다.

전칭긍정의 부정이라고 해서 ‘모든 S는 P가 아니다’라고 하면 안 된다. 왜냐하면 ‘모든 서울 시민은 외계인이 아니다’가 아닌 ‘모든 서울 시민이 외계인은 아니다’라고 한다면 ‘일부 서울 시민은 외계인이 아니다’와 혼동될 우려가 있다.

전칭부정명제는 대문자 E로 표현하기도 한다.

 

특칭긍정명제(Particular affirmative)

어떤 S는 P이다. Some S are P.

예) 어떤 동물은 고양이다. 어떤 음식은 떡볶이다.

특칭긍정명제는 대문자 I로 표현하기도 한다.

 

특칭부정명제(Particular negative)

어떤 S는 P가 아니다. Some S are not P.

예) 어떤 서울 시민은 남성이 아니다. 어떤 책은 만화책이 아니다.

특칭부정명제는 대문자 O로 표현하기도 한다.

 

대당 사각형(the square of opposition)

 

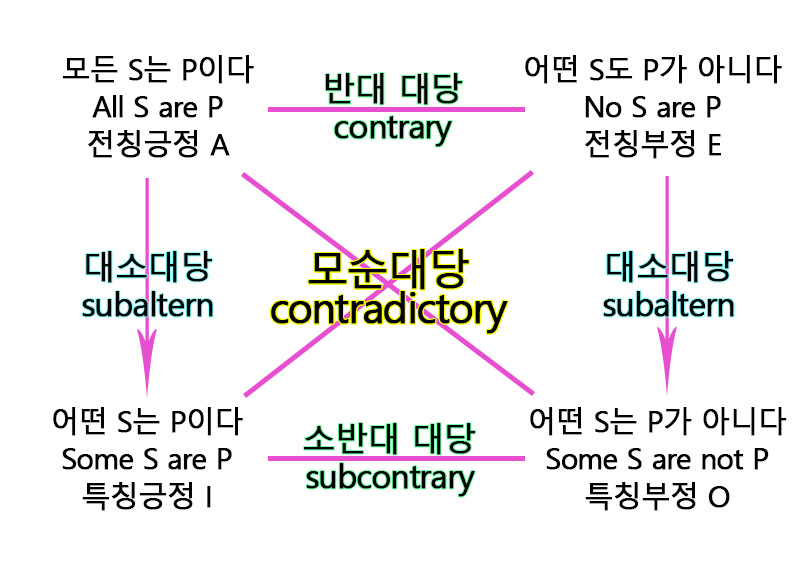모순대당(contradictory)

전칭긍정명제(A)와 특칭부정명제(O), 전칭부정명제(E)와 특칭긍정명제(O)와의 관계다.

두 명제는 동시에 참이거나 거짓일 수 없다. 한 명제가 참이면, 다른 명제는 반드시 거짓이다. 반대로 한 명제가 거짓이라면, 다른 명제는 반드시 참이다.

전칭긍정명제(A)가 참이면, 특칭부정명제(O)는 거짓이다. ‘모든 서울 시민은 사람이다’가 참이라면 ‘어떤 서울 사람은 사람이 아니다’는 거짓이다.

전칭부정명제(E)와 특칭긍정명제(I) 관계도 이와 같다.

 

반대 대당(contrary)

전칭긍정명제(A)와 전칭부정명제(E)와의 관계다.

두 명제는 동시에 참일 수는 없지만 동시에 거짓일 수 있다.

‘모든 강아지는 동물이다'(A)가 참이면 ‘어떤 강아지도 동물이 아니다'(E)는 거짓이다.

‘모든 정치인은 거짓말쟁이다.'(A)가 거짓이면 ‘어떤 정치인도 거짓말쟁이가 아니다'(E)도 거짓일 수 있다.

 

소반대 대당(subcontrary)

특칭긍정명제(I)와 특칭부정명제(O)와의 관계이다.

둘은 동시에 참일 수는 있지만, 동시에 거짓이 될 수는 없다.

‘어떤 서울 시민은 남성이다'(I)가 참이면 ‘어떤 서울 시민은 남성이 아니다'(O)도 참이다.

‘어떤 서울 시민은 사람이다'(I)가 참이면 ‘어떤 서울 시민은 사람이 아니다'(O)는 거짓이다.

‘어떤 여학교 학생은 남성이다'(I)가 거짓이면 ‘어떤 여학교 학생은 남성이 아니다'(O)는 참이다.

 

대소대당(subaltern)

전칭과 특칭과의 관계이다.

전칭이 참이면 특칭도 참이다.

전칭이 거짓이면 특칭은 참 또는 거짓이다.

특칭이 거짓이면 전칭도 거짓이다.

특칭이 참이면 전칭은 참, 또는 거짓이다.

진실은 내려가고 거짓은 올라간다.

 

환위, 환질, 이환

환위(Conversion)

조건문 명제 중 ‘역’에 해당한다.

환위는 정언명제의 주어와 술어를 교환하는 것을 뜻한다.

예를 들어 ‘모든 꽃은 식물이다'(A)의 환위는 ‘모든 식물은 꽃이다’이다.

전칭부정(E)와 특칭긍정(I)이 참이면 환위도 항상 참이다. 거짓이면 환위도 항상 거짓이다.

‘어떤 꽃도 동물이 아니다'(E)가 참이면 환위 ‘어떤 동물도 꽃이 아니다’도 참이다.

‘어떤 식물은 꽃이다'(I)가 참이면 환위 ‘어떤 꽃은 식물이다’도 참이다.

 

환질(Obversion)

조건문 명제 중 ‘이’에 해당한다.

환질은 정언명제의 술어를 여집합으로 바꾸고, 질(긍정, 부정)을 바꾸는 것이다. 술어를 여집합으로 바꿀 때 술어 앞에 ‘비(non)-‘를 붙인다.

‘모든 고래는 포유류이다’ → ‘모든 고래는 비(non) 포유류이다’ → ‘어떤 고래도 비(non) 포유류가 아니다’

환질은 의미상 원래 명제와 차이가 없다.

전칭긍정(A), 전칭부정(E), 특칭긍정(I), 특칭부정(O)이 참이면 그의 환질도 참이다.

 

이환(Contraposition)

조건문 명제 중 ‘대우’에 해당한다.

이환이란 주어와 술어의 위치를 바꾸고, 주어와 술어 각각 여집합으로 바꾸는 것이다.

이환은 환질, 환위, 환질 과정을 거친다.

‘모든 바지는 의류이다’ → ‘어떤 바지도 비(non) 의류가 아니다’ → 어떤 비(non) 의류도 바지가 아니다’ → ‘어떤 비(non) 의류는 비(non) 바지이다’

A, O가 참이면 그 이환도 참이다.

명제 환위 환질 이환
모든 S는 P이다(A)
All S are P		 모든 P는 S이다
All P are S		 어떤 S도 non-P가 아니다
No S are non-P		 모든 non-P는 non-S이다
All non-P are non-S
어떤 S도 P가 아니다(E)
No S are P		 어떤 P도 S가 아니다
No P are S		 모든 S는 non-P이다
All S are non-P		 어떤 non-P도 non-S가 아니다
No non-P are non-S
어떤 S는 P이다(I)
Some S are P		 어떤 P는 S이다
Some P are S		 어떤 S는 non-P가 아니다
Some S are not non-P		 어떤 non-P는 non-S이다
Some non-P are non-S
어떤 S는 P가 아니다(O)
Some S are not P		 어떤 P는 S가 아니다
Some P are not S		 어떤 S는 non-P이다
Some S are non-P		 어떤 non-P는 non-S가 아니다
Some non-P are not non-S

굵은 글씨체는 진리 보존성(truth-preserving)을 갖는다. 진리 보존성이란, 원래 명제가 참이라면, 그 환위, 환질, 또는 이환 역시 참이라는 뜻이다.

 

주연(distribution)

어떤 명제가 주어나 술어의 외연 전체에 대해 판단을 내릴 경우 그 주어나 술어는 ‘주연(周延)’된다고 말하고 외연의 전체가 아닌 일부에 대해서 판단을 내릴 경우 그 주어나 술어는 ‘부주연’된다고 말한다.

분류 명제 주연 or 부주연
주어 술어
A 모든 S는 P이다
All S are P		 주연 부주연
E 어떤 S도 P가 아니다
No S are P		 주연 주연
I 어떤 S는 P이다
Some S are P		 부주연 부주연
O 어떤 S는 P가 아니다
Some S are not P		 부주연 주연

 

벤 다이어그램(Venn diagram)

벤 다이어그램을 사용하여 정언명제를 도식화할 수 있다.

전칭긍정명제(A)

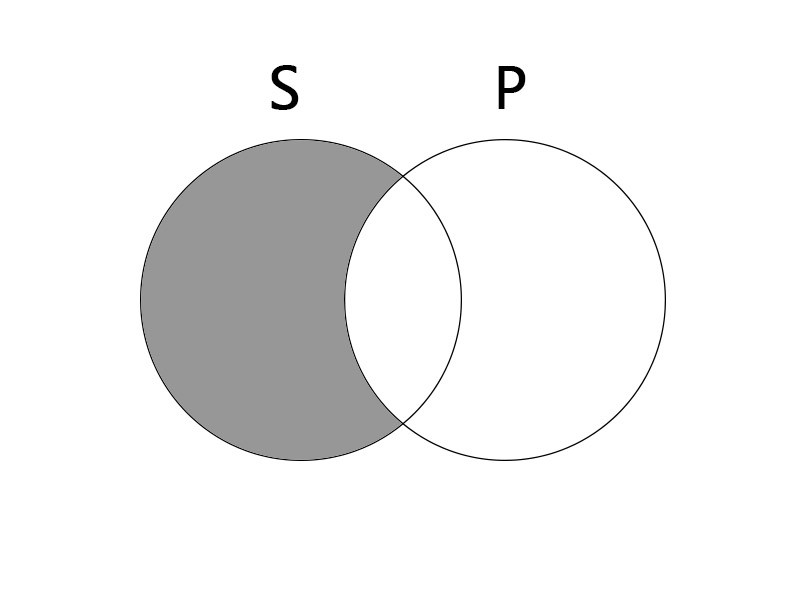모든 S는 P이다. All S are P.

S가 P에 완전히 포함되야 한다. 음영으로 처리된 부분은 아무것도 없은 공집합과 같다.

 

전칭부정명제(E)

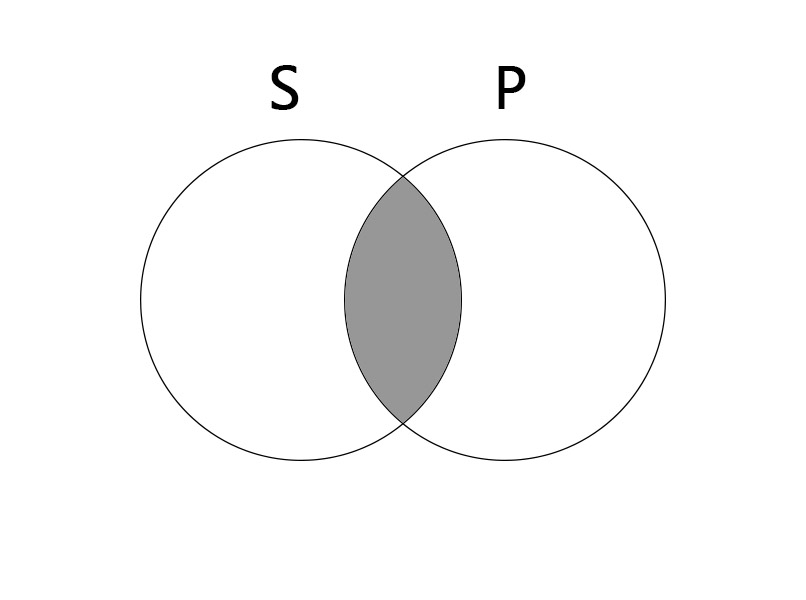어떤 S도 P가 아니다. No S are P.

S와 P 동시에 해당하는 원소가 없기 때문에 가운데 부분이 음영처리 되어 있다.

 

특칭긍정명제(I)

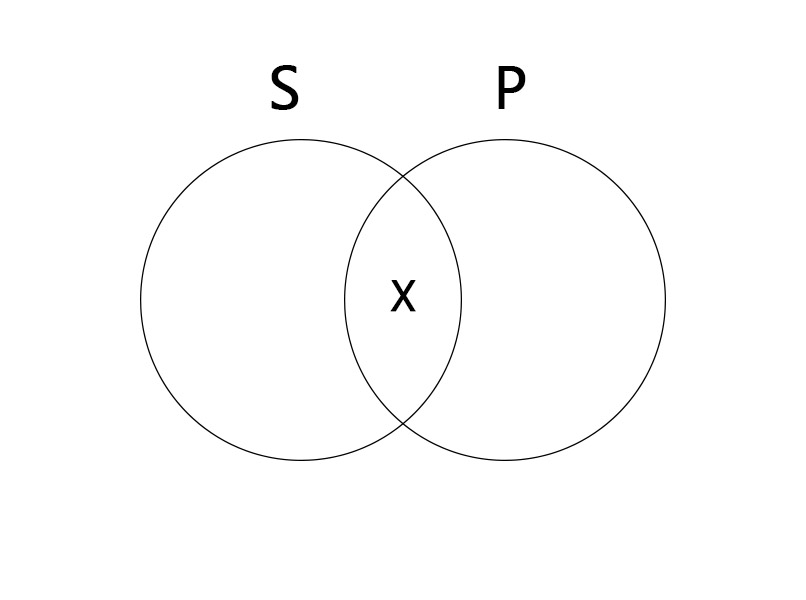어떤 S는 P이다. Some S are P.

일종의 교집합 개념으로 S와 P 동시에 해당하는 원소가 존재한다는 것을 나타내기 위해 S, P 교차 영역에 X 표시를 한다.

 

특칭부정명제(O)

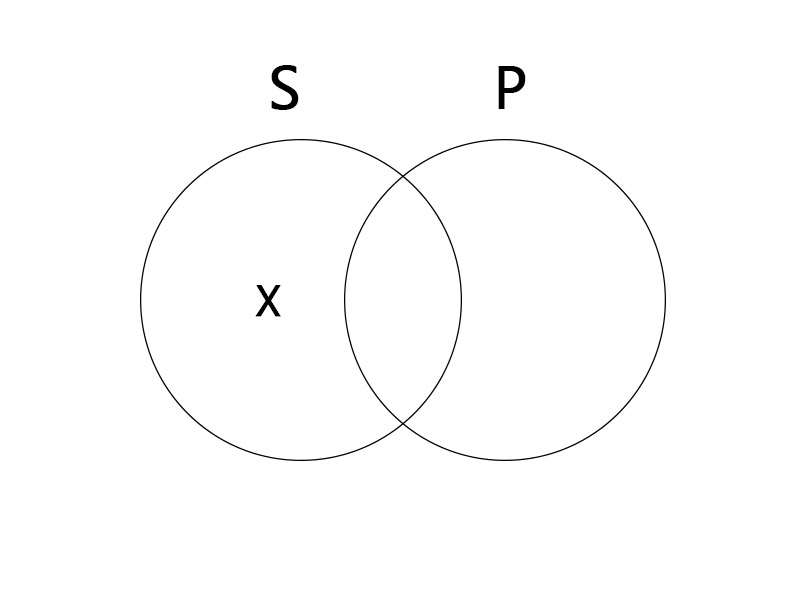어떤 S는 P가 아니다. Some S are not P.

S와 P가 교차하는 영역을 제외한 S 영역에 X 표시를 한다.

 

정언삼단논법(Categorical Syllogism)

정언삼단논법은 정언명제로 이루어진 두 전제를 통해 결론을 도출해내는 논증을 말한다.

전제1: 모든 새는 조류다.
전제2: 어떤 동물은 새다.
결론: 어떤 동물은 조류다.

전칭긍정(A), 전칭부정(E), 특칭긍정(I), 특칭부정(O) 총 네 개의 명제로 256조합이 가능하다. 이 중 타당한 형식은 고전적 해석에 의해 24가지, 현대적 해석에 의해 15가지가 존재한다.

 

구성

정언삼단논법은 대전제-소전제-결론으로 구성된다.

정언삼단논법은 3개의 개념만이 사용된다. 대개념(P), 소개념(S), 매개념(M)이다.

대전제는 대개념이 있는 전제다. 소전제는 소개념이 있는 전제다. 대개념은 결론의 술어가 된다. 소개념은 결론의 주어가 된다. 매개념은 결론 도출을 위한 소개념과 대개념의 매채 역할을 한다.

대전제: 모든 새(매개념(M))는 조류(대개념(P))다.
소전제: 어떤 동물(소개념(S))은 새(매개념(M))다.
결론: 어떤 동물(소개념(S))은 조류(대개념(P))다.

 

정언삼단논법 규칙

  • 3개의 개념만을 가져야 한다.
  • 두 전제에서 매개념이 최소 한 번은 주연되야 한다.
  • 전제에서 주연되지 않은 개념은 결론에서 주연될 수 없다.
  • 부정 명제는 전제에서 최대 한 번 제시되야 한다. 두 전제가 부정 명제이면 결론을 이끌어낼 수 없다.
  • 전제 중 하나가 부정 명제이면 결론도 부정 명제여야 한다.
  • 두 전제가 긍정이면 결론도 긍정이어야 한다.
  • 두 전제가 특칭 명제이면 결론을 이끌어낼 수 없다.
  • 두 전제 중 특칭 명제가 있다면 결론도 특칭 명제여야 한다.
  • 두 전제 모두 전칭 명제라면 결론도 전칭 명제여야 한다.

 

정언삼단논법 유형

정언삼단논법은 일반적으로 4개의 유형으로 나뉜다.

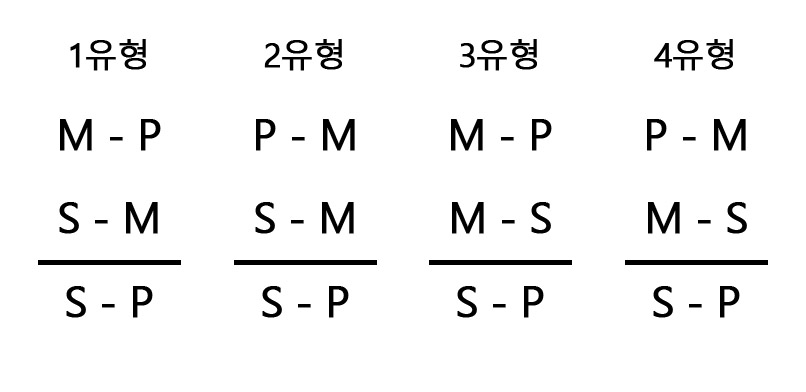결론을 내는 방법은 이와 같다.

 

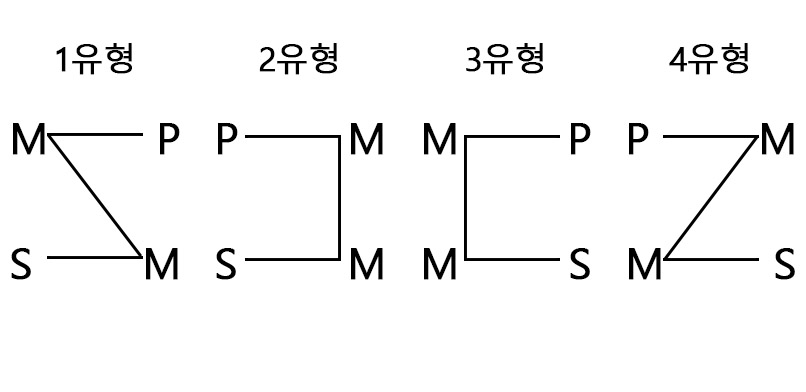타당한 삼단논법 결론

네 개의 정언명제(A, E, I, O)로 만들 수 있는 정언삼단논법은 총 256조합이지만, 이 중 타당한 결론을 가진 유형은 현대적 해석에 의해 총 15가지이다.

1유형 AAA, AII, EAE, EIO
2유형 AEE, AOO, EAE, EIO
3유형 AII, EIO, IAI, OAO
4유형 AEE, EIO, IAI

벤 다이어그램을 통해 도식화하여 결론을 도출한다.

벤 다이어그램으로 결론을 도출할 때에는 전칭명제 먼저 도식화한다.

 

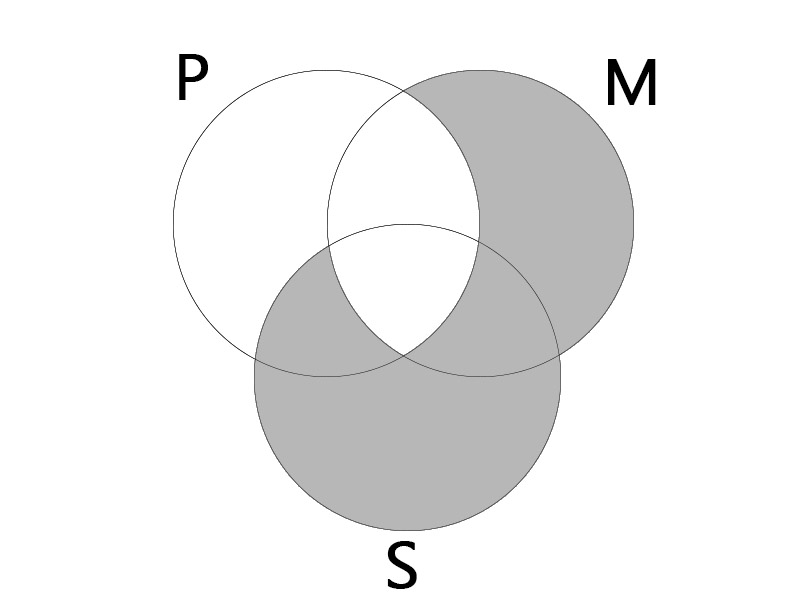
1유형

AAA

대전제: 모든 M은 P이다. (All M is P.)
소전제: 모든 S는 M이다. (All S is M.)
결론: 모든 S는 P이다. (All S is P.)

 

AII

대전제: 모든 M은 P이다. (All M is P.)
소전제: 어떤 S는 M이다. (Some S is M.)
결론: 어떤 S는 P이다. (Some S is P.)

 

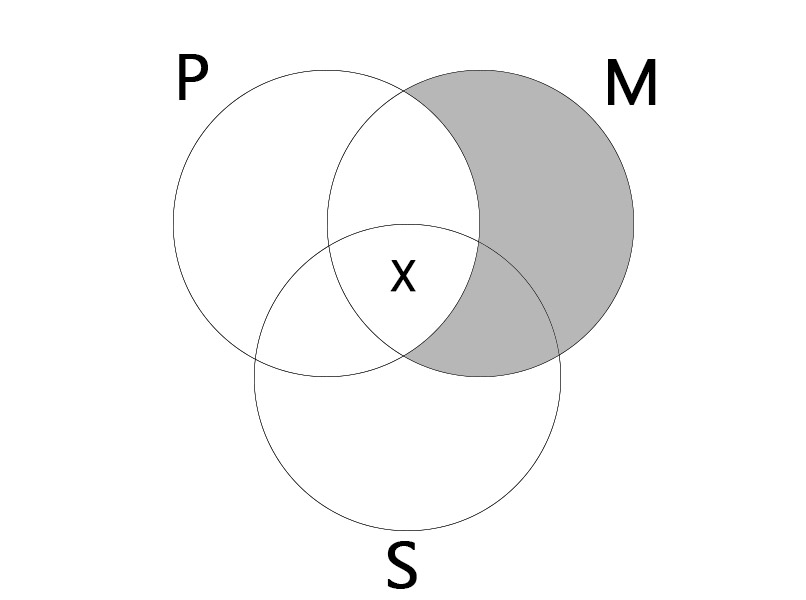EAE

대전제: 어떤 M도 P가 아니다. (No M is P.)
소전제: 모든 S는 M이다. (All S is M.)
결론: 어떤 S도 P가 아니다. (All S is P.)

 

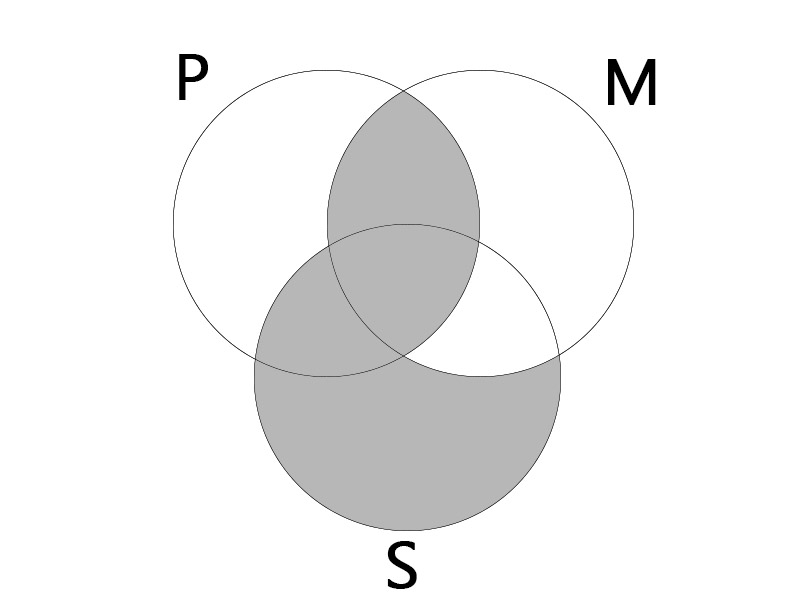EIO

대전제: 어떤 M도 P가 아니다. (No M is P.)
소전제: 어떤 S는 M이다. (Some S is M.)
결론: 어떤 S는 P가 아니다. (Some S is not P.)

 

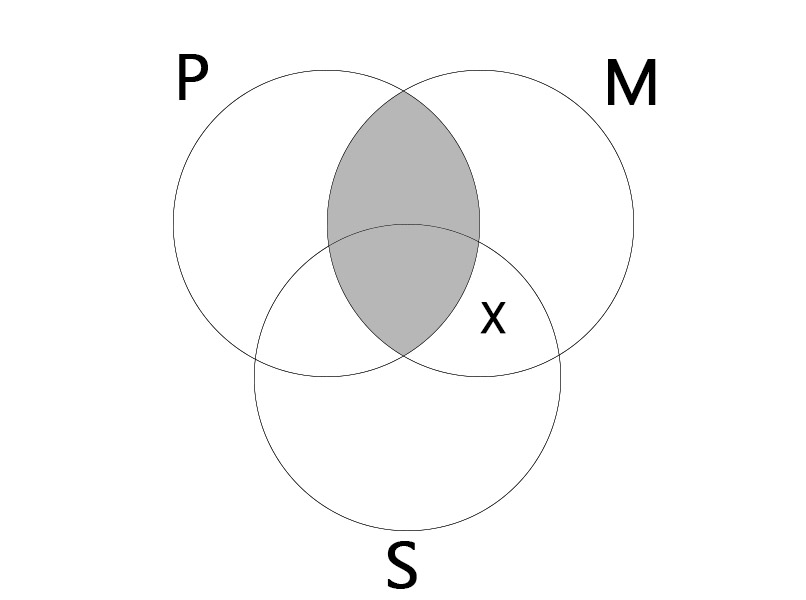2유형

AEE

대전제: 모든 P는 M이다. (All P is M.)
소전제: 어떤 S도 M가 아니다. (No S is M.)
결론: 어떤 S도 P가 아니다. (No S is P.)

 

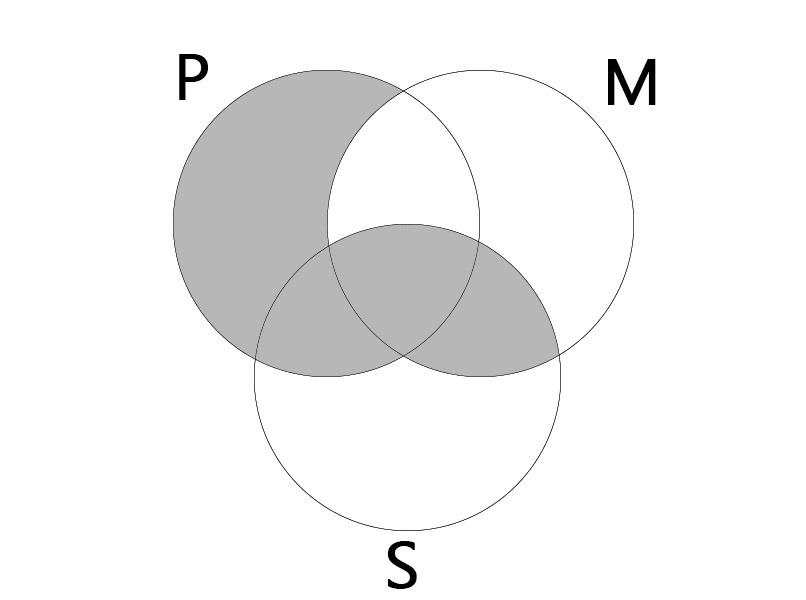AOO

대전제: 모든 P는 M이다. (All P is M.)
소전제: 어떤 S는 M가 아니다. (Some S is not M.)
결론: 어떤 S는 P가 아니다. (Some S is not P.)

 

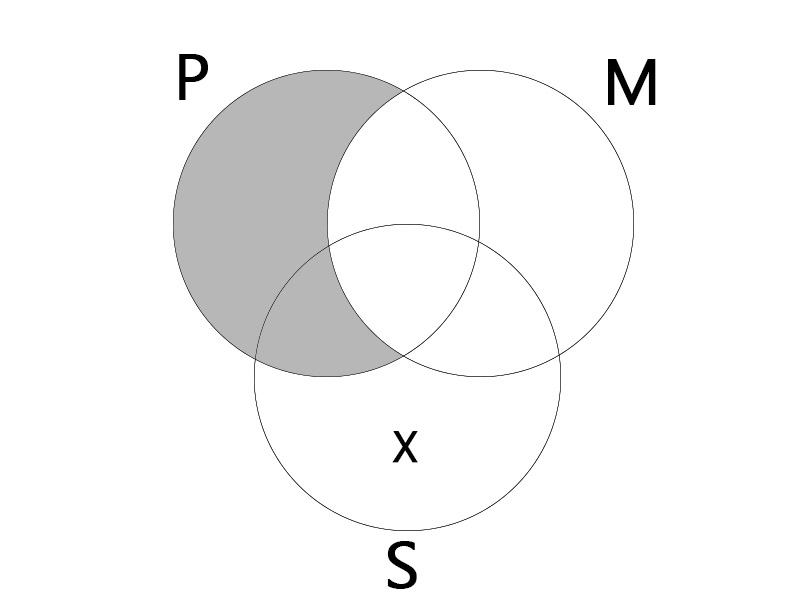EAE

대전제: 어떤 P도 M가 아니다. (No P is M.)
소전제: 모든 S는 M이다. (All S is M.)
결론: 어떤 S도 P가 아니다. (No S is P.)

 

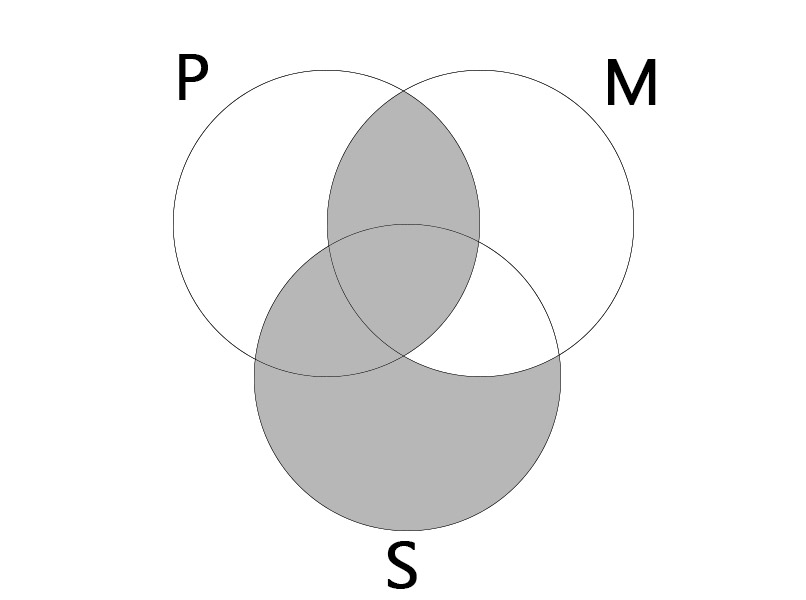EIO

대전제: 어떤 P도 M가 아니다. (No P is M.)
소전제: 어떤 S는 M이다. (Some S is M.)
결론: 어떤 S는 P가 아니다. (Some S is not P.)

 

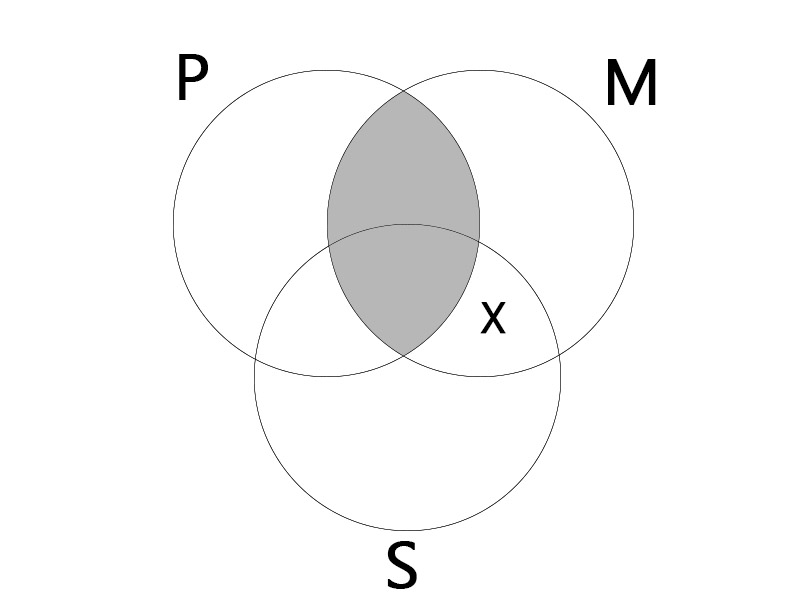3유형

AII

대전제: 모든 M은 P이다. (All M is P.)
소전제: 어떤 M은 S이다. (Some M is S.)
결론: 어떤 S는 P이다. (Some S is P.)

 

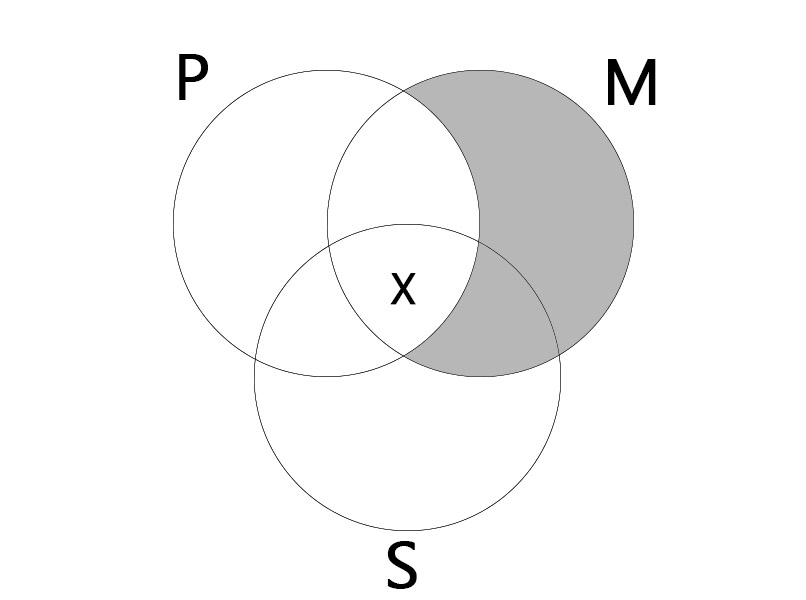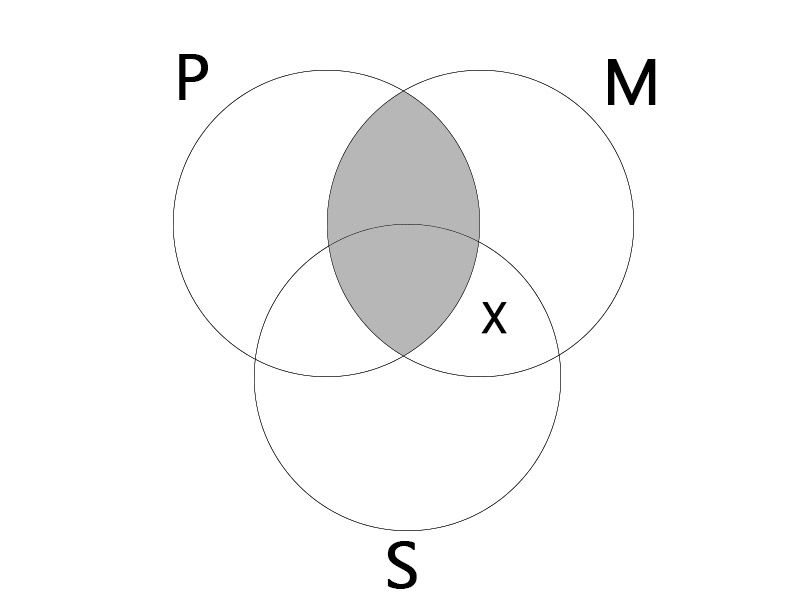
EIO

대전제: 어떤 M도 P가 아니다. (No M is P.)
소전제: 어떤 M은 S이다. (Some M is S.)
결론: 어떤 S는 P가 아니다. (Some S is not P.)

 

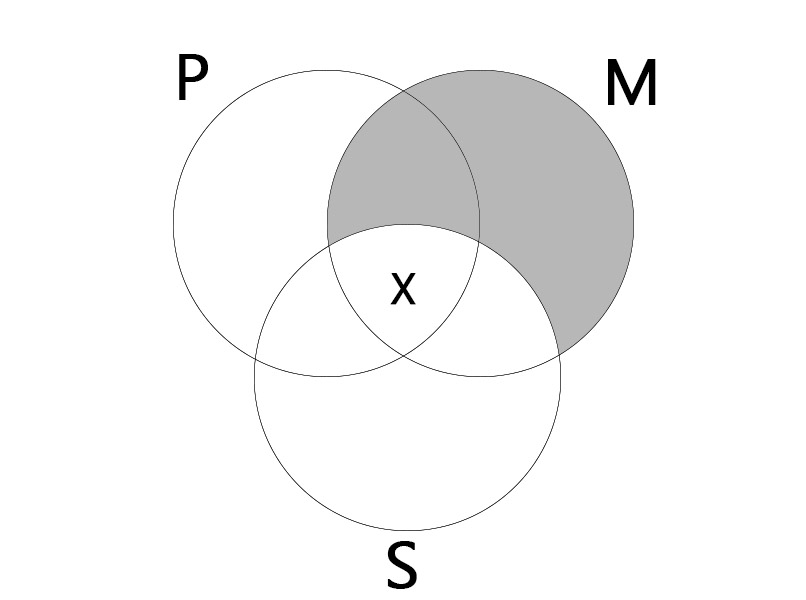
IAI

대전제: 어떤 M은 P이다. (Some M is P.)
소전제: 모든 M은 S이다. (All M is S.)
결론: 어떤 S는 P이다. (Some S is P.)

 

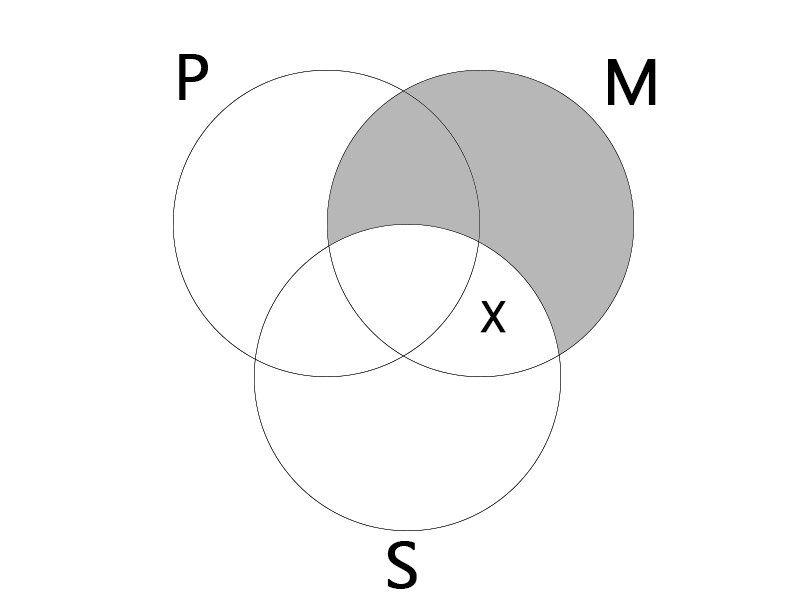
OAO

대전제: 어떤 M은 P가 아니다. (Some M is not P.)
소전제: 모든 M은 S이다. (All M is S.)
결론: 어떤 S는 P가 아니다. (Some S is not P.)

 

4유형

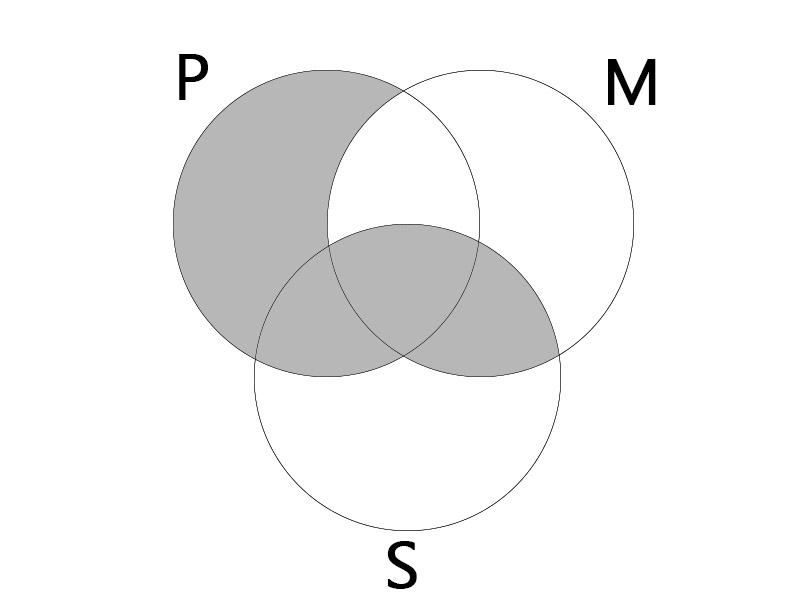
AEE

대전제: 모든 P는 M이다. (All P is M.)
소전제: 어떤 M도 S가 아니다. (No M is S.)
결론: 어떤 S도 P가 아니다. (No S is P.)

 

EIO

대전제: 어떤 P도 M가 아니다. (No P is M.)
소전제: 어떤 M은 S이다. (Some M is S.)
결론: 어떤 S는 P가 아니다. (Some S is not P.)

 

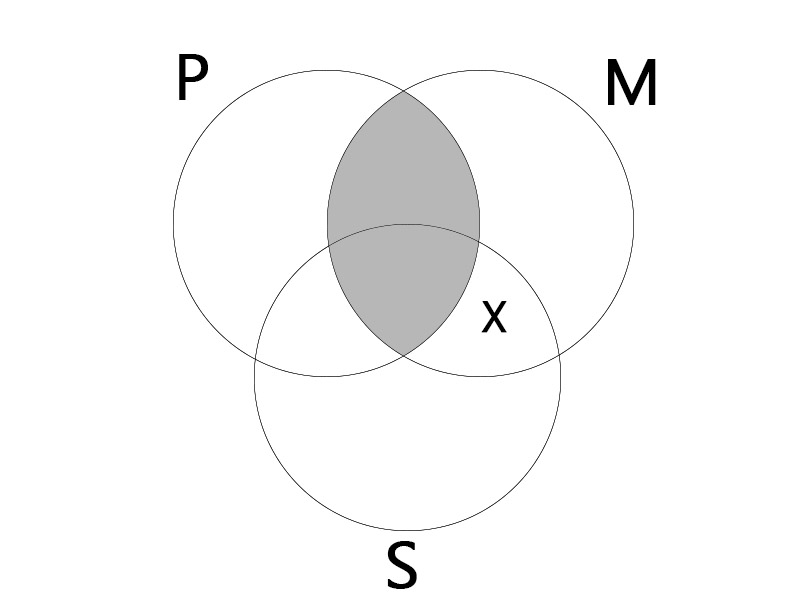IAI

대전제: 어떤 P는 M이다. (Some P is M.)
소전제: 모든 M은 S이다. (All M is S.)
결론: 어떤 S는 P이다. (Some S is P.)

 

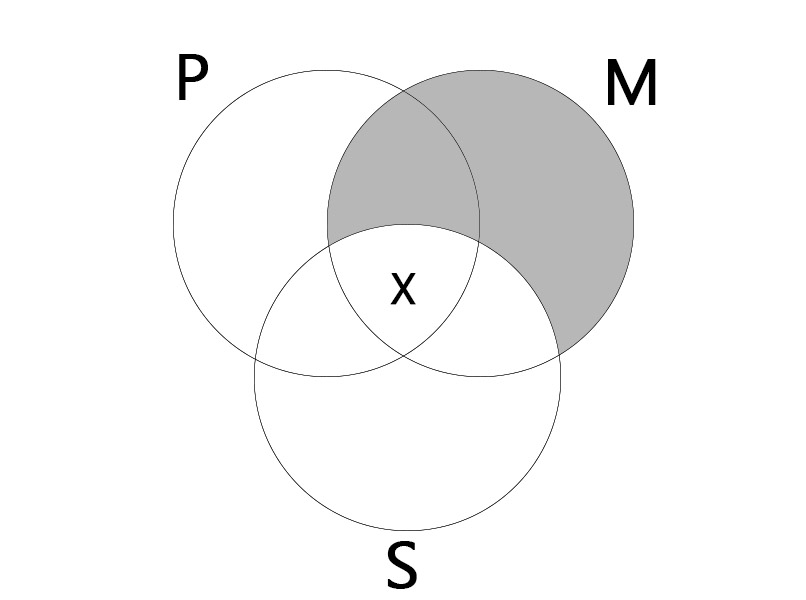고전적 해석에 의한 타당한 정언삼단논법

고전적 해석에 의한 타당한 정언삼단논법에 위 15가지를 제외한 다음 9가지가 추가된다.

1유형 AAI, EAO
2유형 AEO, EAO
3유형 AAI, EAO
4유형 AEO, EAO, AAI

 

정언삼단논법 오류

이외 정언삼단논법에서 발생하는 오류는 위 정언삼단논법 규칙을 지키지 않아 발생한다.

정언논리 공부자료

정언논리 기출문제

답글 남기기

이메일 주소는 공개되지 않습니다. 필수 필드는 *로 표시됩니다