[PSAT 기출] 2020 5급 상황판단 나책형 13번 해설 – 시계 주사위 시계 문자판 말판 말 짝수 홀수 확률 논리퀴즈

1 개요
2 문제
3 문제 해설
4 2020 5급 PSAT 상황판단
5 관련 문서

개요

다음은 2020년 국가공무원 5급 상황판단영역 나책형 13번 문제 해설이다.

문제

문 13. 다음 글을 근거로 판단할 때, <보기>에서 옳은 것만을 모두 고르면?

甲과 乙은 시계와 주사위를 이용한 게임을 하며, 규칙은 다음과 같다.

○ 1~12시까지 적힌 시계 문자판을 말판으로 삼아, 1개의 말을 12시에 놓고 게임을 시작한다.

○ 주사위를 던져 짝수가 나오면 말을 시계 방향으로 1시간 이동시키며, 홀수가 나오면 말을 반시계 방향으로 1시간 이동시킨다.

○ 甲과 乙이 번갈아 주사위를 각 12번씩 총 24번 던져 말의 최종 위치로 게임의 승자를 결정한다.

○ 말의 최종 위치가 1~5시이면 甲이 승리하고, 7~11시이면 乙이 승리한다. 6시 또는 12시이면 무승부가 된다.

<보 기>

ㄱ. 말의 최종 위치가 3시일 확률은 \(\dfrac{\text{1}}{\text{12}}\)이다.

ㄴ. 말의 최종 위치가 4시일 확률과 8시일 확률은 같다.

ㄷ. 乙이 마지막 주사위를 던질 때, 홀수가 나오는 것보다 짝수가 나오는 것이 甲에게 항상 유리하다.

ㄹ. 乙이 22번째 주사위를 던져 말을 이동시킨 결과 말의 위치가 12시라면, 甲이 승리할 확률은 무승부가 될 확률보다 낮다.

① ㄱ, ㄷ

② ㄴ, ㄷ

③ ㄴ, ㄹ

④ ㄷ, ㄹ

⑤ ㄱ, ㄴ, ㄹ

출처: 사이버국가고시센터

문제 해설

ㄱ. 말의 최종 위치가 3시일 확률은 \(\dfrac{\text{1}}{\text{12}}\)이다.

짝수와 홀수의 조합이 (12, 12)이면 말의 위치는 12시다.

짝수와 홀수의 조합이 (13, 11)이면 말의 위치는 2시다.

짝수와 홀수의 조합이 (14, 10)이면 말의 위치는 4시다.

주사위를 총 24번 던지기 때문에 짝수와 홀수의 조합에 상관 없이 말의 위치는 짝수 숫자이다.

그러므로 말의 최종 위치가 3시일 확률은 0이다.

따라서 보기의 내용은 옳지 않다.

ㄴ. 말의 최종 위치가 4시일 확률과 8시일 확률은 같다.

말의 최종 위치가 4시인 짝수와 홀수의 조합은 (2, 22), (8, 16), (14, 10), (20, 4)이다.

말의 최종 위치가 8시인 짝수와 홀수의 조합은 (22, 2), (16, 8), (10, 14), (4, 20)이다.

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24
짝/홀	짝	짝	홀	홀	홀	홀	홀	홀	홀	홀	홀	홀	홀	홀	홀	홀	홀	홀	홀	홀	홀	홀	홀	홀

주사위를 던져 짝수와 홀수가 나올 각각 확률은 \(\dfrac{\text{1}}{\text{2}}\)이다.

주사위를 던져 짝수가 첫 번째와 두 번째에만 나온다면 (2, 22) 조합을 만족하여 말의 최종 위치는 4시가 된다. 이렇게 나올 확률은 \((\dfrac{\text{1}}{\text{2}})^{24}\)이다.

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24
짝/홀	홀	홀	홀	홀	홀	홀	홀	홀	홀	홀	홀	짝	홀	홀	짝	홀	홀	홀	홀	홀	홀	홀	홀	홀

(2, 22) 조합은 여러 개가 가능하다. 위와 같이 12번째, 15번째에 짝수가 나와도 (2, 22) 조합을 만족한다.

주사위를 24번 던져 짝수가 2번 나오는 경우의 수는 ₂₄C₂ = \(\dfrac{\text{24×23}}{\text{2×1}}\) = 276가지이다.

주사위를 24번 던져 짝수가 2번 나올 확률은 \(\dfrac{_{24}C_2}{2^{24}}\)이다.

그렇다면 주사위를 24번 던져 (2, 22), (8, 16), (14, 10), (20, 4)의 조합을 만족할 확률은

\(\dfrac{_{24}C_{2}+_{24}C_{8}+_{24}C_{14}+_{24}C_{20}}{2^{24}}\)이다. 이것은 말의 최종 위치가 4시일 확률이다.

한편, 말의 최종 위치가 8시일 확률은 주사위를 24번 던져 (22, 2), (16, 8), (10, 14), (4, 20) 조합을 만족할 확률과 같으므로,

\(\dfrac{_{24}C_{22}+_{24}C_{16}+_{24}C_{10}+_{24}C_{4}}{2^{24}}\)이다.

수학적으로,_a+bC_a = _a+bC_b이다. 즉 ₂₄C₂와 ₂₄C₂₂는 같다.

그러므로 \(\dfrac{_{24}C_{2}+_{24}C_{8}+_{24}C_{14}+_{24}C_{20}}{2^{24}}\) = \(\dfrac{_{24}C_{22}+_{24}C_{16}+_{24}C_{10}+_{24}C_{4}}{2^{24}}\)이다.

즉, 말의 최종 위치가 4시일 확률과 8시일 확률은 같다.

따라서 보기의 내용은 옳다.

ㄷ. 乙이 마지막 주사위를 던질 때, 홀수가 나오는 것보다 짝수가 나오는 것이 甲에게 항상 유리하다.

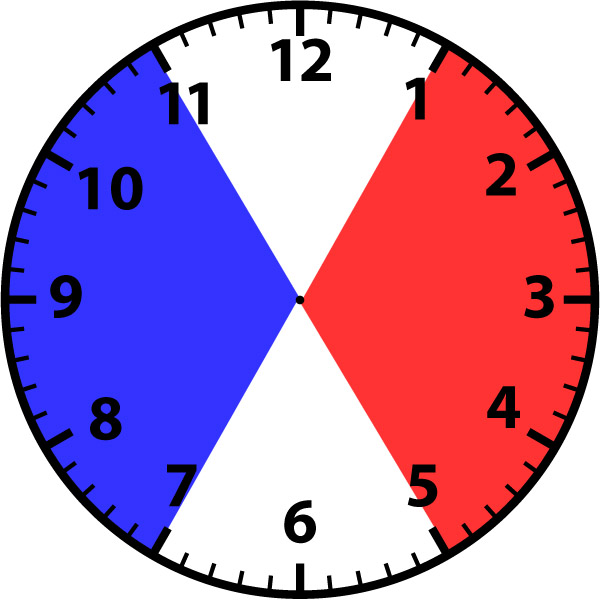乙이 마지막 주사위를 던진다는 것은 현재까지 23번의 주사위를 던졌다는 뜻이다. 23번의 주사위를 던졌다면 말은 항상 홀수 시간에 있다.

말의 최종 위치가 1~5시이면 甲이 승리하고, 7~11시이면 乙이 승리한다.

현재 말의 위치가 1시라면, 마지막 주사위를 던졌을 때 짝수가 나오면 말의 최종위치가 2시가 되어 甲이 승리한다.

현재 말의 위치가 5시라면, 마지막 주사위를 던졌을 때 짝수가 나오면 말의 최종위치가 6시가 되어 무승부가 된다.

현재 말의 위치가 7시라면, 마지막 주사위를 던졌을 때 짝수가 나오면 말의 최종위치가 8시가 되어 乙이 승리한다.

현재 말의 위치가 11시라면, 마지막 주사위를 던졌을 때 짝수가 나오면 말의 최종위치가 12시가 되어 무승부가 된다.

그러므로 乙이 마지막 주사위를 던질 때, 홀수가 나오는 것보다 짝수가 나오는 것이 甲에게 항상 유리한 것은 아니다.

따라서 보기의 내용은 옳지 않다.

ㄹ. 乙이 22번째 주사위를 던져 말을 이동시킨 결과 말의 위치가 12시라면, 甲이 승리할 확률은 무승부가 될 확률보다 낮다.

	23	24	최종위치
홀/짝	홀	홀	10시(乙)
	홀	짝	12시(무승부)
	짝	홀	12시(무승부)
	짝	짝	2시(甲)

甲이 승리할 확률은 \(\dfrac{\text{1}}{\text{4}}\)이고, 무승부일 확률은 \(\dfrac{\text{2}}{\text{4}}=\dfrac{\text{1}}{\text{2}}\)이다.

따라서 보기의 내용은 옳다.

정답은 ③번이다.

개요

문제

문제 해설

2020 5급 PSAT 상황판단

관련 문서

답글 남기기 응답 취소