[PSAT 기출] 2020 5급 자료해석 나책형 33번 34번 해설 – 건설업 재해 재해자 수 재해율

1 개요
2 문제
3 33번 문제 해설
4 34번 문제 해설
5 2020 5급 PSAT 자료해석
6 관련 문서

개요

다음은 2020년 국가공무원 5급 자료해석영역 나책형 33번, 34번 문제 해설이다.

문제

※ 다음 <표>와 <그림>은 2013~2019년 ‘갑’국의 건설업 재해에 관한 자료이다. <표>와 <그림>을 보고 물음에 답하시오. [문 33.~문 34.]

<표> 연도별 건설업 재해 현황 (단위: 명)
연도	근로자 수	재해자 수
연도	근로자 수	재해자 수	사망자 수
2013	3,200,645	22,405	611
2014	3,087,131	22,845	621
2015	2,776,587	23,323	496
2016	2,586,832	( )	667
2017	3,249,687	23,723	486
2018	3,358,813	( )	493
2019	3,152,859	26,484	554

<그림 1> 연도별 전체 산업 및 건설업 재해율 추이

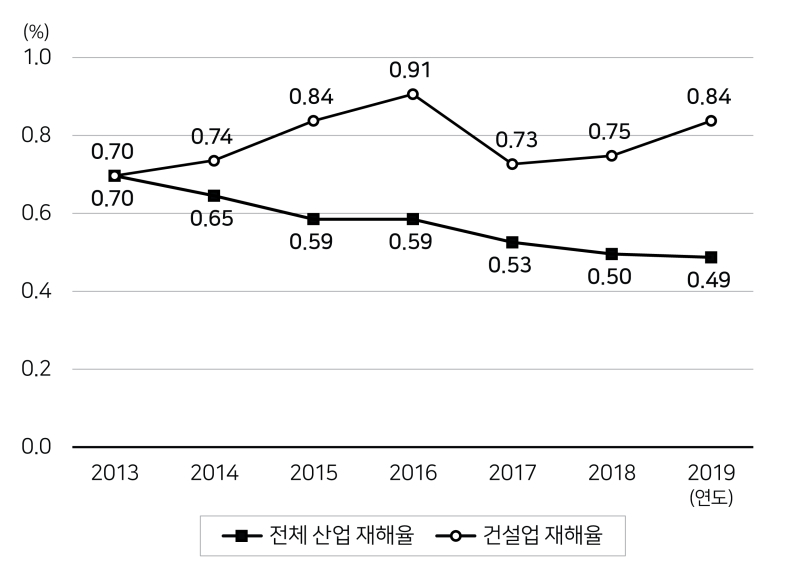※ 재해율(%)＝\(\dfrac{\text{재해자 수}}{\text{근로자 수}}\)×100

<그림 2> 연도별 건설업의 환산도수율과 환산강도율

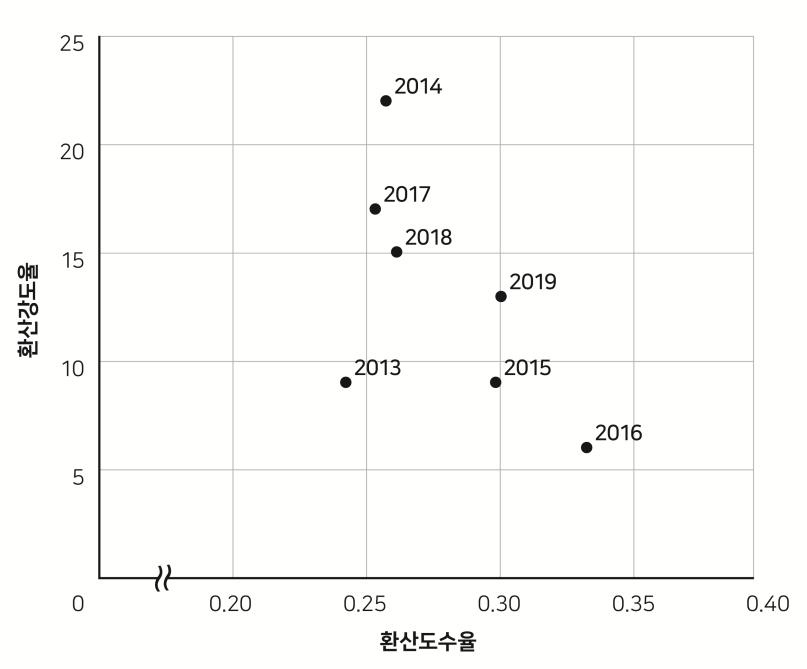※ 1) 환산도수율＝\(\dfrac{\text{재해건수}}{\text{총 근로시간}}\)×100,000

2) 환산강도율＝\(\dfrac{\text{재해손실일수}}{\text{총 근로시간}}\)×100,000

문 33. 위 <표>와 <그림>에 근거한 설명으로 옳은 것은?

① 건설업 재해자 수는 매년 증가한다.

② 전체 산업 재해율과 건설업 재해율의 차이가 가장 큰 해는 2016년이다.

③ 2020년 건설업 재해자 수가 전년 대비 10% 증가한다면, 건설업 재해율은 전년 대비 0.1%p 증가할 것이다.

④ 2013년 건설업 근로자 수가 전체 산업 근로자 수의 20%라면, 전체 산업 재해자 수는 건설업 재해자 수의 4배이다.

⑤ 건설업 사망자 수가 가장 많은 해는 건설업 환산강도율도 가장 높다.

문 34. 위 <표>와 <그림>을 바탕으로 건설업의 재해건당 재해손실일수가 가장 큰 연도와 가장 작은 연도를 바르게 나열한 것은?

	가장 큰 연도	가장 작은 연도
①	2013년	2014년
②	2013년	2016년
③	2014년	2013년
④	2014년	2016년
⑤	2016년	2014년

출처: 사이버국가고시센터

33번 문제 해설

① 건설업 재해자 수는 매년 증가한다.

<표> 연도별 건설업 재해 현황 (단위: 명)
연도	근로자 수	재해자 수
연도	근로자 수	재해자 수	사망자 수
2013	3,200,645	22,405	611
2014	3,087,131	22,845	621
2015	2,776,587	23,323	496
2016	2,586,832	( )	667
2017	3,249,687	23,723	486
2018	3,358,813	( )	493
2019	3,152,859	26,484	554

2016년 건설업 재해율: 0.91%

2016년 재해자 수: 2,586,832명 × 0.91% ≒ 23,540명

2018년 건설업 재해율: 0.75%

2018년 재해자 수: 3,358,813명 × 0.75% ≒ 25,191명

건설업 재해자 수는 매년 증가한다.

따라서 보기의 내용은 옳다.

② 전체 산업 재해율과 건설업 재해율의 차이가 가장 큰 해는 2016년이다.

2016년 전체 산업 재해율과 건설업 재해율의 차이: 0.91%-0.59% = 0.32%

2018년 전체 산업 재해율과 건설업 재해율의 차이: 0.84%-0.49% = 0.35%

전체 산업 재해율과 건설업 재해율의 차이가 가장 큰 해는 2018년이다.

따라서 보기의 내용은 옳지 않다.

③ 2020년 건설업 재해자 수가 전년 대비 10% 증가한다면, 건설업 재해율은 전년 대비 0.1%p 증가할 것이다.

2020년의 근로자 수를 알 수 없기 때문에 재해율을 증감 여부를 알 수 없다.

따라서 보기의 내용은 옳지 않다.

④ 2013년 건설업 근로자 수가 전체 산업 근로자 수의 20%라면, 전체 산업 재해자 수는 건설업 재해자 수의 4배이다.

2013년 전체 산업 및 건설업 재해율은 0.70%로 같다.

그러므로 2013년 건설업 근로자 수가 전체 산업 근로자 수의 20%라면, 건설업 재해자 수 역시 전체 산업 재해자 수의 20%가 된다.

20%의 역수는 5가 되므로 4배가 아니라 5배이다.

따라서 보기의 내용은 옳지 않다.

⑤ 건설업 사망자 수가 가장 많은 해는 건설업 환산강도율도 가장 높다.

건설업 사망자 수가 가장 많은 해는 2016년 667명이다.

한편, 건설업 환산강도율도 가장 높은 해는 2014년이다.

따라서 보기의 내용은 옳지 않다.

정답은 ①번이다.

34번 문제 해설

재해건당 재해손실일수는 \(\dfrac{\text{재해손실일수}}{\text{재해건수}}\)가 된다.

환산강도율＝\(\dfrac{\text{재해손실일수}}{\text{총 근로시간}}\)×100,000

환산도수율＝\(\dfrac{\text{재해건수}}{\text{총 근로시간}}\)×100,000

\(\dfrac{\text{환산강도율}}{\text{환산도수율}}\)=\(\dfrac{\dfrac{\text{재해손실일수}}{\text{총 근로시간}}×100,000}{\dfrac{\text{재해건수}}{\text{총 근로시간}}×100,000}\)이므로, \(\dfrac{\text{환산강도율}}{\text{환산도수율}}\)=\(\dfrac{\text{재해손실일수}}{\text{재해건수}}\)가 된다.

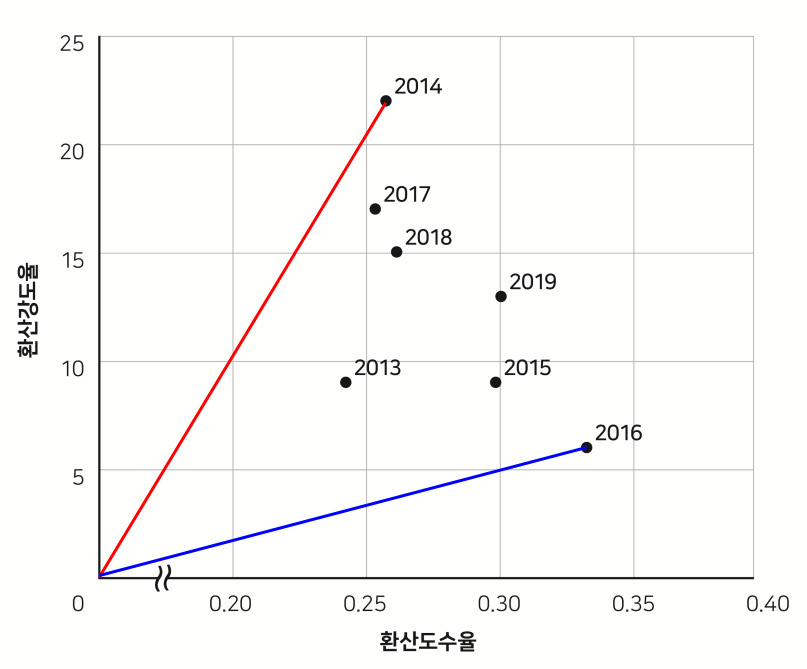\(\dfrac{\text{환산강도율}}{\text{환산도수율}}\)은 위 그래프에서 원점에서 각 점까지 그은 직선의 기울기가 된다.

재해건당 재해손실일수가 크다는 것은 \(\dfrac{\text{환산강도율}}{\text{환산도수율}}\)의 값, 즉 기울기가 크다는 것을 의미한다.

기울기가 가장 큰 직선을 빨간선이고, 가장 작은 직선은 파란선이다.

재해건당 재해손실일수가 가장 큰 연도는 2014년이고, 제일 작은 연도는 2016년이다.

정답은 ④번이다.

개요

문제

33번 문제 해설

34번 문제 해설

2020 5급 PSAT 자료해석

관련 문서

답글 남기기 응답 취소