[PSAT 기출] 2024 5급 자료해석 나책형 14번 해설 – A 미술전 응모인원

1 개요
2 문제
3 문제 해설
4 2024 5급 PSAT 자료해석
5 관련 문서

개요

다음은 2024년 국가공무원 5급 자료해석영역 나책형 14번 문제 해설이다.

문제

14. 다음 <표>와 <그림>은 A 미술전 응모 및 수상 결과에 관한 자료이다. 이에 대한 <보기>의 설명 중 옳은 것만을 모두 고르면?

<표> 2023년 A 미술전 응모 및 수상 결과 (단위: 개, 명)
부문 구분	초등부		중등부		고등부
	팀		팀		팀
		인원		인원		인원
응모	268	502	232	446	306	624
수상	56	88	30	59	43	68
※ A미술전의 부문은 초등부, 중등부, 고등부로만 구성됨.

<그림> 연도별 A미술전 응모인원

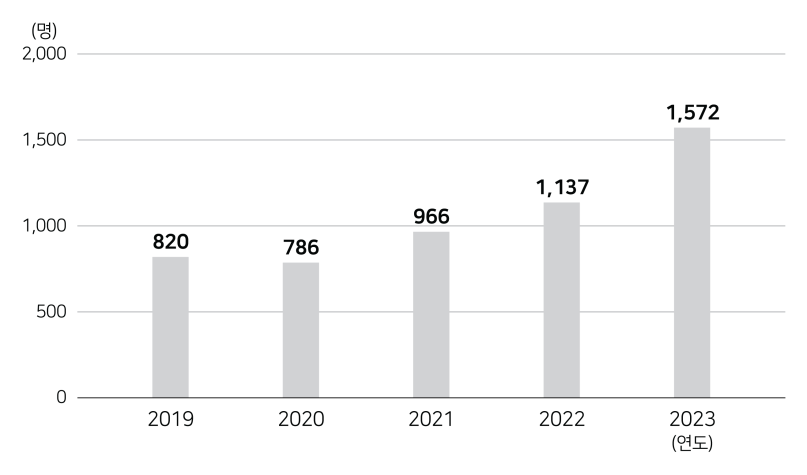<보 기>

ㄱ. 2023년 응모인원 대비 수상인원이 가장 많은 부문은 초등부이다.

ㄴ. 2023년 팀별 인원이 1~3명이라면, 3명으로 구성된 초등부 수상팀은 15개 이하이다.

ㄷ. 2020년 응모인원의 부문별 구성비가 2023년과 동일하다면, 2020년 중등부 응모인원은 200명 이상이다.

ㄹ. 2024년부터 매년 응모인원이 전년 대비 30%씩 증가한다면, 응모인원이 2019년의 3배를 처음 초과하는 해는 2026년이다.

① ㄱ, ㄴ

② ㄱ, ㄷ

③ ㄴ, ㄷ

④ ㄴ, ㄹ

⑤ ㄱ, ㄷ, ㄹ

출처: 사이버국가고시센터

문제 해설

ㄱ. 2023년 응모인원 대비 수상인원이 가장 많은 부문은 초등부이다.

<표> 2023년 A 미술전 응모 및 수상 결과 (단위: 개, 명)
부문 구분	초등부		중등부		고등부
	팀		팀		팀
		인원		인원		인원
응모	268	502	232	446	306	624
수상	56	88	30	59	43	68
※ A미술전의 부문은 초등부, 중등부, 고등부로만 구성됨.

초등부 응모인원 대비 수상인원: \(\dfrac{\text{268}}{\text{502}}\) ≒ 53.4%

중등부 응모인원 대비 수상인원: 52.0%

고등부 응모인원 대비 수상인원: 49.0%

따라서 보기의 내용은 옳다.

ㄴ. 2023년 팀별 인원이 1~3명이라면, 3명으로 구성된 초등부 수상팀은 15개 이하이다.

<표> 2023년 A 미술전 응모 및 수상 결과 (단위: 개, 명)
부문 구분	초등부		중등부		고등부
	팀		팀		팀
		인원		인원		인원
응모	268	502	232	446	306	624
수상	56	88	30	59	43	68
※ A미술전의 부문은 초등부, 중등부, 고등부로만 구성됨.

인원이 1명인 팀의 수: X개

인원이 2명인 팀의 수: Y개

인원이 3명인 팀의 수: Z개

X + 2Y + 3Z = 88명 … ①

X + Y + Z = 56개 … ②

①식에서 ②식을 빼면, Y + 2Z = 32가 된다.

2023년 팀별 인원이 1~3명이라고 했을 뿐, 초등부에서 수상한 팀별 인원이 빠짐없이 1명, 2명, 3명으로 이루어졌는지는 알 수 없다.

Y + 2Z = 32에서 인원이 2명인 Y팀 수가 0개이라면 인원이 3명인 Z팀의 최대 수는 16개가 된다.

그러므로 3명으로 구성된 초등부 수상팀이 16개 이하이다.

따라서 보기의 내용은 옳지 않다.

ㄷ. 2020년 응모인원의 부문별 구성비가 2023년과 동일하다면, 2020년 중등부 응모인원은 200명 이상이다.

<표> 2023년 A 미술전 응모 및 수상 결과 (단위: 개, 명)
부문 구분	초등부		중등부		고등부
	팀		팀		팀
		인원		인원		인원
응모	268	502	232	446	306	624
수상	56	88	30	59	43	68
※ A미술전의 부문은 초등부, 중등부, 고등부로만 구성됨.

<그림> 연도별 A미술전 응모인원

2020년 응모인원: 786명

2020년 중등부 응모인원 구성비: \(\dfrac{\text{446명}}{\text{1,572명}}\)

2020년 중등부 응모인원: \(\dfrac{\text{446명}}{\text{1,572명}}×\text{786명}\) ≒ 223명

따라서 보기의 내용은 옳다.

ㄹ. 2024년부터 매년 응모인원이 전년 대비 30%씩 증가한다면, 응모인원이 2019년의 3배를 처음 초과하는 해는 2026년이다.

<그림> 연도별 A미술전 응모인원

2019년 응모인원 3배: 820명 × 3배 = 2,460명

2024년 응모인원: 1,572명 × 1.3 = 2,044명

2025년 응모인원: 2,044명 × 1.3 = 2,657명

응모인원이 2019년의 3배를 처음 초과하는 해는 2025년이다.

따라서 보기의 내용은 옳지 않다.

정답은 ②번이다.

개요

문제

문제 해설

2024 5급 PSAT 자료해석

관련 문서

답글 남기기 응답 취소