[PSAT 기출] 2016 5급 자료해석 4책형 4번 해설 – 원주 등분점 자연수 대응선

1 개요
2 문제
3 문제 해설
4 2016 5급 PSAT 자료해석
5 관련 문서

개요

다음은 2016년 국가공무원 5급 자료해석영역 4책형 4번 문제 해설이다.

문제

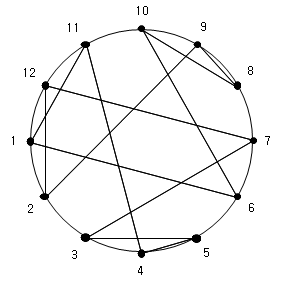
문 4. 영희가 다음의 <규칙>에 따라 아래의 <그림>을 작성하였을 때, 영희가 사용한 두 자연수 n과 m의 합을 구하면?

<규 칙>

○ 원주를 (n－1) 등분하여 ‘등분점’을 찍는다.

○ ‘등분점’ 중 임의의 한 점부터 반시계 방향으로 각 점에 순서대로 1, 2, …, n－1의 번호를 붙인다.

○ 임의의 ‘등분점’ P를 선택해 P의 번호에 m을 곱한 수를 n으로 나눈 나머지를 구하여, 그 값을 번호로 가지는 ‘등분점’을 P의 ‘대응점’이라 한다. 단, \(2≤m≤\dfrac{\text{n}}{\text{2}}\)이다.

○ 각 ‘등분점’과 그 ‘등분점’의 ‘대응점’을 선으로 연결한다.

<그 림>

① 15

② 16

③ 17

④ 18

⑤ 19

출처: 사이버국가고시센터

문제 해설

n – 1 = 12이므로 n = 13이다.

n과 m의 합을 구하므로 보기에서 13을 빼서 m의 후보값을 구한다.

m의 후보값은 2, 3, 4, 5, 6이 된다.

m = 2일 때

(1 × 2) ÷ 13: 나머지 = 2

위 그림에서 1과 2는 대응선으로 연결되지 않는다.

따라서 m = 2가 아니다.

m = 3일 때

(1 × 3) ÷ 13: 나머지 = 3

위 그림에서 1과 3은 대응선으로 연결되지 않는다.

따라서 m = 3이 아니다.

m = 4일 때

(1 × 4) ÷ 13: 나머지 = 4

위 그림에서 1과 4는 대응선으로 연결되지 않는다.

따라서 m = 4가 아니다.

m = 5일 때

(1 × 5) ÷ 13: 나머지 = 5

위 그림에서 1과 5는 대응선으로 연결되지 않는다.

따라서 m = 5가 아니다.

m = 6일 때

(1 × 6) ÷ 13: 나머지 = 6

위 그림에서 1과 6은 대응선으로 연결된다.

(7 × 6) ÷ 13: 나머지 = 3

위 그림에서 7과 3은 대응선으로 연결된다.

(12 × 6) ÷ 13: 나머지 = 7

위 그림에서 12과 7은 대응선으로 연결된다.

따라서 m = 6이다.

정답은 ⑤번이다.

개요

문제

문제 해설

2016 5급 PSAT 자료해석

관련 문서

답글 남기기 응답 취소