[PSAT 기출] 2015 5급 자료해석 인책형 40번 해설 – 마을 이동로 확률

1 개요
2 문제
3 문제 해설
4 2015 5급 PSAT 자료해석
5 관련 문서

개요

다음은 2015년 국가공무원 5급 자료해석영역 인책형 40번 문제 해설이다.

문제

문 40. 아래 <그림>은 마을 A~E 간의 가능 이동로를 보여주며, <표>는 주어진 <조건>에 따라 ‘갑’이 매 회차 이동 후 각 마을에 숨어있을 확률을 구한 자료이다. 이에 대한 <보기>의 설명 중 옳은 것만을 모두 고르면?

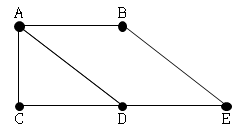
<그림> 마을 A~E 간 가능 이동로

<조 건>

○ 1회차 이동 후 ‘갑’이 각 마을(A~E)에 숨어있을 확률은 각각 \(\dfrac{\text{1}}{\text{5}}\)로 동일하다.

○ ‘갑’은 2회차부터 매 회차, 숨어있던 마을에서 인접한 마을로 반드시 이동하며, 이 때 인접한 마을이란 다른 마을을 경유하지 않고 가능 이동로만으로 이동할 수 있는 마을을 의미한다. 예를 들어 B와 인접한 마을은 A, E이다.

○ ‘갑’이 인접한 마을로 이동시 각 마을로 이동할 확률은 동일하다.

<표> 매 회차 이동 후 ‘갑’이 각 마을에 숨어있을 확률

마을 이동차수	A	B	C	D	E
1회차	\(\dfrac{\text{1}}{\text{5}}\)	\(\dfrac{\text{1}}{\text{5}}\)	\(\dfrac{\text{1}}{\text{5}}\)	\(\dfrac{\text{1}}{\text{5}}\)	\(\dfrac{\text{1}}{\text{5}}\)
2회차	\(\dfrac{\text{4}}{\text{15}}\)	\(\dfrac{\text{1}}{\text{6}}\)	\(\dfrac{\text{2}}{\text{15}}\)	\(\dfrac{\text{4}}{\text{15}}\)	\(\dfrac{\text{1}}{\text{6}}\)
3회차	\(\dfrac{\text{43}}{\text{180}}\)	\(\dfrac{\text{31}}{\text{180}}\)	( )	\(\dfrac{\text{43}}{\text{180}}\)	\(\dfrac{\text{31}}{\text{180}}\)
4회차	\(\dfrac{\text{55}}{\text{216}}\)	( )	( )	( )	( )

※예) 3회차 이동 후 ‘갑’이 B에 숨어있을 확률＝(2회차 이동 후 A에 숨어있을 확률×A에서 B로 이동할 확률)＋(2회차 이동 후 E에 숨어있을 확률×E에서 B로 이동할 확률)＝(\(\dfrac{\text{4}}{\text{15}}\) × \(\dfrac{\text{1}}{\text{3}}\)) + (\(\dfrac{\text{1}}{\text{6}}\) × \(\dfrac{\text{1}}{\text{2}}\)) = \(\dfrac{\text{31}}{\text{180}}\)

<보 기>

ㄱ. ‘갑’이 A에 숨어있을 확률은 1회차 이동 후부터 3회차 이동 후까지 매 회차 증가하였다.

ㄴ. ‘갑’이 C에 숨어있을 확률은 3회차 이동 후보다 4회차이동 후가 더 낮다.

ㄷ. 4회차 이동 후 ‘갑’이 B에 숨어있을 확률과 E에 숨어있을 확률은 동일하다.

ㄹ. 3회차 이동 후 ‘갑’이 숨어있을 확률이 가장 낮은 곳은 C이다.

① ㄱ, ㄴ

② ㄱ, ㄷ

③ ㄴ, ㄷ

④ ㄴ, ㄹ

⑤ ㄷ, ㄹ

출처: 사이버국가고시센터

문제 해설

ㄱ. ‘갑’이 A에 숨어있을 확률은 1회차 이동 후부터 3회차 이동 후까지 매 회차 증가하였다.

갑이 1회차 이동 후 A에 숨어있을 확률: \(\dfrac{\text{1}}{\text{5}}=\dfrac{\text{36}}{\text{180}}\)

갑이 2회차 이동 후 A에 숨어있을 확률: \(\dfrac{\text{4}}{\text{15}}=\dfrac{\text{48}}{\text{180}}\)

갑이 4회차 이동 후 A에 숨어있을 확률: \(\dfrac{\text{43}}{\text{180}}\)

갑’이 A에 숨어있을 확률은 2회차 이동 후까지 증가하다가 3회차 이동 후에는 감소하였다.

따라서 보기의 내용은 옳지 않다.

ㄴ. ‘갑’이 C에 숨어있을 확률은 3회차 이동 후보다 4회차이동 후가 더 낮다.

C에 인접한 마을은 A와 D이다.

갑이 n회차 이동 후에 C에 숨어있을 확률은 ((n-1)회차 이동 후 A에 숨어있을 확률×A에서 D로 이동할 확률)＋((n-1)회차 이동 후 D에 숨어있을 확률×D에서 C로 이동할 확률)이다.

갑이 3회차 이동 후에 C에 숨어있을 확률: (\(\dfrac{\text{4}}{\text{15}}\) × \(\dfrac{\text{1}}{\text{3}}\)) + (\(\dfrac{\text{4}}{\text{15}}\) × \(\dfrac{\text{1}}{\text{3}}\)) = \(\dfrac{\text{8}}{\text{45}}= \dfrac{\text{48}}{\text{270}}\)

갑이 4회차 이동 후에 C에 숨어있을 확률: (\(\dfrac{\text{43}}{\text{180}}\) × \(\dfrac{\text{1}}{\text{3}}\)) + (\(\dfrac{\text{43}}{\text{180}}\) × \(\dfrac{\text{1}}{\text{3}}\)) = \(\dfrac{\text{43}}{\text{270}}\)

따라서 보기의 내용은 옳다.

ㄷ. 4회차 이동 후 ‘갑’이 B에 숨어있을 확률과 E에 숨어있을 확률은 동일하다.

B에 인접한 마을은 A와 E이다.

E에 인접한 마을은 D와 B이다.

갑이 4회차 이동 후에 B에 숨어있을 확률은 (3회차 이동 후 A에 숨어있을 확률×A에서 B로 이동할 확률)＋(3회차 이동 후 E에 숨어있을 확률×E에서 B로 이동할 확률)이다.

갑이 4회차 이동 후에 E에 숨어있을 확률은 (3회차 이동 후 D에 숨어있을 확률×D에서 E로 이동할 확률)＋(3회차 이동 후 B에 숨어있을 확률×B에서 E로 이동할 확률)이다.

갑이 4회차 이동 후에 B에 숨어있을 확률: (\(\dfrac{\text{43}}{\text{180}}\) × \(\dfrac{\text{1}}{\text{3}}\)) + (\(\dfrac{\text{31}}{\text{180}}\) × \(\dfrac{\text{1}}{\text{2}}\))

갑이 4회차 이동 후에 E에 숨어있을 확률: (\(\dfrac{\text{43}}{\text{180}}\) × \(\dfrac{\text{1}}{\text{3}}\)) + (\(\dfrac{\text{31}}{\text{180}}\) × \(\dfrac{\text{1}}{\text{2}}\))

4회차 이동 후 ‘갑’이 B에 숨어있을 확률과 E에 숨어있을 확률은 동일하다.

따라서 보기의 내용은 옳다.

ㄹ. 3회차 이동 후 ‘갑’이 숨어있을 확률이 가장 낮은 곳은 C이다.

보기 ㄴ에 따르면 3회차 이동 후 ‘갑’이 C에 숨어있을 확률은 \(\dfrac{\text{8}}{\text{45}}= \dfrac{\text{32}}{\text{180}}\)이다.

반면 3회차 이동 후 ‘갑’이 B와 E에 숨어있을 확률은 \(\dfrac{\text{31}}{\text{180}}\)이다.

3회차 이동 후 ‘갑’이 숨어있을 확률이 가장 낮은 곳은 B와 E이다.

따라서 보기의 내용은 옳지 않다.

정답은 ③번이다.

개요

문제

문제 해설

2015 5급 PSAT 자료해석

관련 문서

답글 남기기 응답 취소