[PSAT] 국가직 7급 모의평가 상황판단 13번 – 우편번호 논리퀴즈

1 개요
2 문제
3 문제 해설
4 PSAT 국가직 7급 모의평가 상황판단
5 관련 문서

개요

다음은 국가직 7급 PSAT 모의평가 상황판단영역 13번 문제다.

문제

문 13. 다음 글을 근거로 판단할 때, 올바른 우편번호의 첫자리와 끝자리 숫자의 합은?

다섯 자리 자연수로 된 우편번호가 있다. 甲과 乙은 실수로 ‘올바른 우편번호’에 숫자 2를 하나 추가하여 여섯 자리로 표기하였다. 甲은 올바른 우편번호의 끝자리 뒤에 2를 추가하였고, 乙은 올바른 우편번호의 첫자리 앞에 2를 추가하였다. 그 결과 甲이 잘못 표기한 우편번호 여섯 자리 수는 乙이 잘못 표기한 우편번호 여섯 자리 수의 3배가 되었다.

올바른 우편번호와 甲과 乙이 잘못 표기한 우편번호는 아래와 같다.

○ 올바른 우편번호: □□□□□

○ 甲이 잘못 표기한 우편번호: □□□□□2

○ 乙이 잘못 표기한 우편번호: 2□□□□□

① 11

② 12

③ 13

④ 14

⑤ 15

출처: 사이버국가고시센터

문제 해설

올바른 우편번호를 abcde라고 가정.

甲이 잘못 표기한 우편번호: abcde2

乙이 잘못 표기한 우편번호: 2abcde

甲이 잘못 표기한 우편번호 여섯 자리 수는 乙이 잘못 표기한 우편번호 여섯 자리 수의 3배:

2abcde × 3 = abcde2

숫자 e: 끝자리 e에 3을 곱하면 3 × e = □2가 된다. e에 0부터 9까지 숫자를 대입하면 □2가 되는 것은 숫자는 4밖에 없다. 따라서 e는 4가 된다.

숫자 a: 2abcde × 3 = abcde2 이기 때문에 숫자 a는 최소 6이된다. 乙이 잘못 표기한 우편번호 첫자리 2에 3을 곱하면 6이 되고, 둘째 자리 a × 3에서 올라온 십의 자리가 있다면 6 이상이 될 수 있기 때문이다.

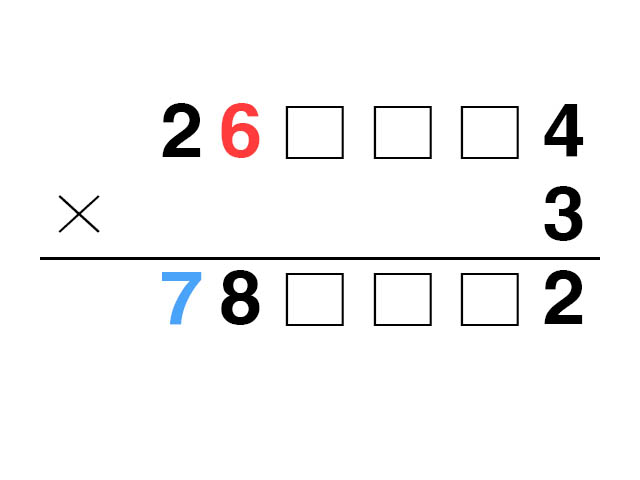
a를 6이라고 가정하자.

乙이 잘못 표기한 우편번호 둘째자리에 3을 곱하면 18이 되고 첫자리에 1이 추가되어 甲이 잘못 표기한 우편번호 첫자리가 7이 된다. 그러면 甲과 乙이 잘못 표기한 우편번호의 숫자 a가 달라지게 된다.

더군다나 乙이 잘못 표기한 우편번호 셋째자리가 9가 된다면 둘째자리에 2를 더해야 하고 최종적으로 첫자리는 8이 되어 차이가 더 발생한다.

따라서 a는 6이 아니다.

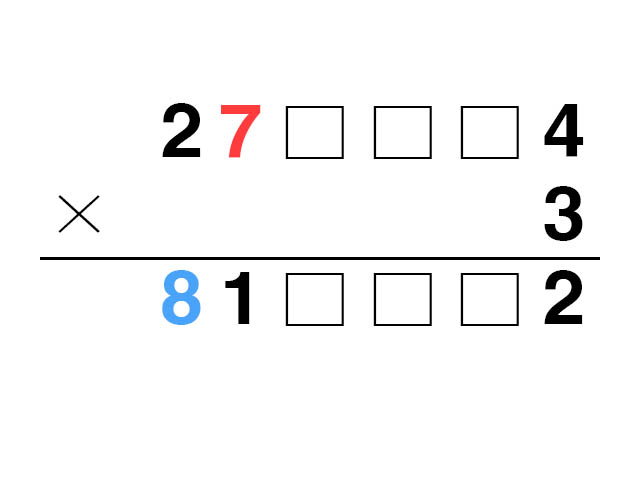
a를 7이라고 가정하자.

乙이 잘못 표기한 우편번호 둘째자리에 3을 곱하면 21이 되고 첫자리에 2가 추가되어 甲이 잘못 표기한 우편번호 첫자리가 8이 된다. 그러면 甲과 乙이 잘못 표기한 우편번호의 숫자 a가 달라지게 된다.

乙이 잘못 표기한 우편번호 셋째자리가 9가 된다고 해도 첫자리가 8이라는 것은 변함이 없다.

따라서 a는 7이 아니다.

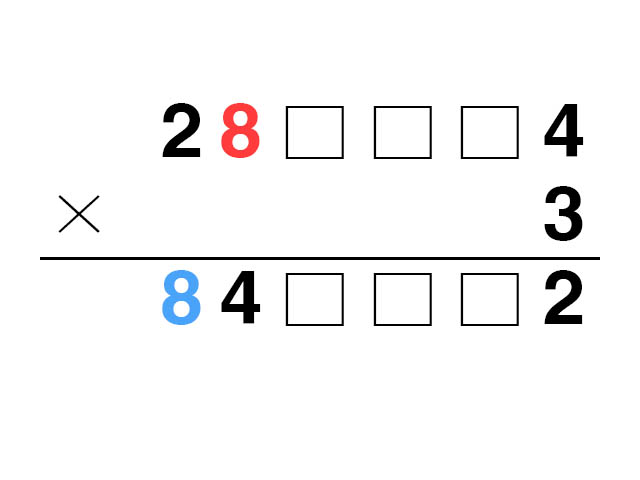
a를 8이라고 가정하자.

乙이 잘못 표기한 우편번호 둘째자리에 3을 곱하면 24이 되고 첫자리에 2가 추가되어 甲이 잘못 표기한 우편번호 첫자리가 8이 된다. 그러면 甲과 乙이 잘못 표기한 우편번호의 숫자 a가 같아지게 된다.

乙이 잘못 표기한 우편번호 셋째자리가 9가 된다고 해도 첫자리가 8이라는 것은 변함없다.

따라서 a는 8이다.

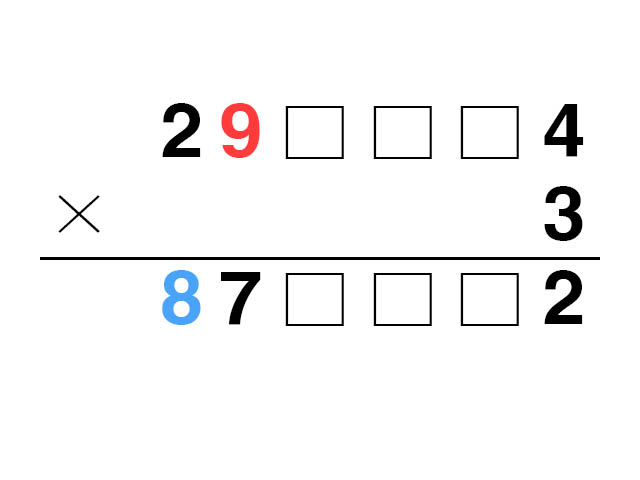
a를 9라고 가정하자.

乙이 잘못 표기한 우편번호 둘째자리에 3을 곱하면 27이 되고 첫자리에 2가 추가되어 甲이 잘못 표기한 우편번호 첫자리가 8이 된다. 그러면 甲과 乙이 잘못 표기한 우편번호의 숫자 a가 달라지게 된다.

乙이 잘못 표기한 우편번호 셋째자리가 9가 된다고 해도 첫자리가 8이라는 것은 변함없다.

따라서 a는 9가 아니다.

a와 e의 합은 8 + 4 = 12가 된다.

정답은 ②번이다.

개요

문제

문제 해설

PSAT 국가직 7급 모의평가 상황판단

관련 문서

답글 남기기 응답 취소